服务热线
搜题▪组卷
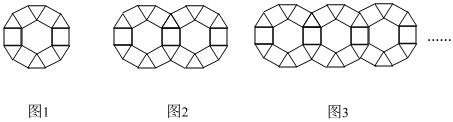
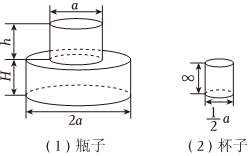 图(1)的瓶子中盛满了水,如果将这个瓶子中的水全部倒入图(2)的杯子中,请回答以下问题.(单位:cm)
图(1)的瓶子中盛满了水,如果将这个瓶子中的水全部倒入图(2)的杯子中,请回答以下问题.(单位:cm)
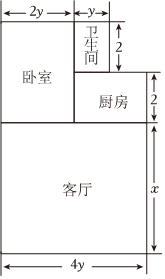 小王准备给家里的地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题.
小王准备给家里的地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题. 如图,某学校要利用围墙建一长方形的自行车存车场ABCD,其它三面用护栏围起来,其中BC的长为(2m+n)米,AB比BC短(n-m)米.
如图,某学校要利用围墙建一长方形的自行车存车场ABCD,其它三面用护栏围起来,其中BC的长为(2m+n)米,AB比BC短(n-m)米.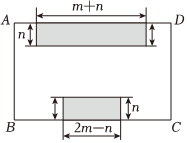 陕北秧歌在今年春节期间又一次火遍全网,让全国各地百姓了解到陕北人民的豪爽气魄.如图,陕北某市计划在一块长方形公园空地上建造一个秧歌观赏台(阴影部分).
陕北秧歌在今年春节期间又一次火遍全网,让全国各地百姓了解到陕北人民的豪爽气魄.如图,陕北某市计划在一块长方形公园空地上建造一个秧歌观赏台(阴影部分).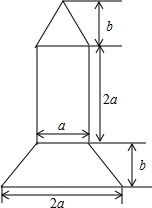 为庆祝我国首个空间实验室“天宫一号”顺利升空,学校开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
为庆祝我国首个空间实验室“天宫一号”顺利升空,学校开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.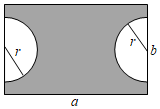 如图所示,某公司打算将一长方形空地美化,并在左右两边各修一个半圆形的花坛,其余部分(图中阴影部分)种草.已知长方形的长为a米,宽为b米,半圆半径为r米(2r<b).(结果保留π)
如图所示,某公司打算将一长方形空地美化,并在左右两边各修一个半圆形的花坛,其余部分(图中阴影部分)种草.已知长方形的长为a米,宽为b米,半圆半径为r米(2r<b).(结果保留π)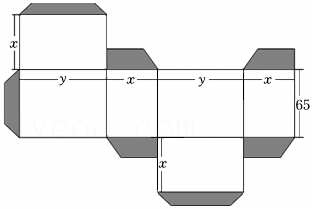
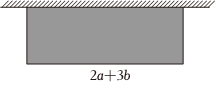 如图,学校要利用专款建一长方形的电动车停车场,其他三面用护栏围起,其中长方形停车场的长为(2a+3b)米,宽比长少(a-b)米.
如图,学校要利用专款建一长方形的电动车停车场,其他三面用护栏围起,其中长方形停车场的长为(2a+3b)米,宽比长少(a-b)米.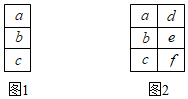 观察下列三行数:
观察下列三行数: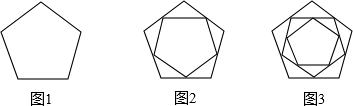
| 图形标号 | 1 | 2 | 3 |
| 正五边形个数 | |||
| 三角形个数 |

ynb@dyw.com
2024-11-18
初中数学 | 七年级上 | 解答题