某市据实际情况主要采取以下四种扶贫方式第一以工代赈方式指政府投资建设基础设施工程组织贫困地区群众参加工程建设并获得劳务报酬第二整村推进方式指以贫困村为具体帮扶对象帮扶对口到村资金安排到村扶贫效益到户第三科技扶贫方式指组织科技人员深入贫困乡村实地指导技术培训等传授科技知识第四移民搬迁方式指对目前极少数居住在生存条件恶劣自然资源贫乏地区的特困人口实行自愿移民该市为了年更好的完成精准扶贫各项任务年初在全市贫困户分一般贫困户和五特户两类中随机抽取了

首页 > 试题列表 > 单题解析

169718. （2023•师大附中•高一下期末）某市据实际情况主要采取以下四种扶贫方式：第一，以工代赈方式，指政府投资建设基础设施工程，组织贫困地区群众参加工程建设并获得劳务报酬，第二，整村推进方式指以贫困村为具体帮扶对象，帮扶对口到村，资金安排到村，扶贫效益到户，第三，科技扶贫方式，指组织科技人员深入贫困乡村实地指导、技术培训等传授科技知识，第四，移民搬迁方式，指对目前极少数居住在生存条件恶劣、自然资源贫乏地区的特困人口，实行自愿移民，该市为了2020年更好的完成精准扶贫各项任务，2020年初在全市贫困户（分一般贫困户和“五特”户两类）中随机抽取了5000户就目前的主要四种扶贫方式行了问卷调查，支持每种扶贫方式的结果如表：

调查的贫困户	支持以工代赈户数	支持整村推进户数	支持科技扶贫户数	支持移民搬迁户数
一般贫困户	1200	1600	b	200
五特户（五保户和特困户）	100	a	c	100

已知在被调查的5000户中随机抽取一户支持整村推进的概率为0.36．
（Ⅰ）现用分层抽样的方法在所有参与调查的贫困户中抽取50户进行深入访谈，问应在支持科技扶贫户数中抽取多少户？
（Ⅱ）虽然“五特”户在全市的贫困户所占比例不大，但本次调查要有意义，其中这次调查的“五特”户户数不能低于被调查总户数的9.2%，已知b≥1530，c≥58，求本次调查有意义的概率是多少？

共享时间:2023-07-17 难度:2

纠错

下载

相似

组卷白板

[考点]

古典概型及其概率计算公式，分层随机抽样，

[答案]

（Ⅰ）16户；（Ⅱ）

．

[解析]

解：（Ⅰ）∵支持整村推进户数为5000×0.36＝1800户．
∴b+c＝5000﹣1200﹣100﹣1800﹣300＝1600户．
∴应在支持科技扶贫户数中抽取的户数为：

（户）．
（Ⅱ）∵a＝200
五特户户数不能低于被调查总户数的9.2%，
∴即5000×9.2%＝460，
∴c≥60有意义，又b≥1530，c≥58，b+c＝1600，b，c情况列举如下：
（1530，70），（1531，69），（1532，68），（1533，67），（1534，66），（1535，65），（1536，64），（1537，63），（1538，62），（1539，61），（1540，60），（1541，59），（1542，58）共13种情况．
∴本次调查有意义的概率

．

[点评]

本题考查了"古典概型及其概率计算公式，分层随机抽样，"，属于"易错题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

168527. （2021•西安中学•六模）一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如表（单位：辆）：

	轿车A	轿车B	轿车C
舒适型	100	150	z
标准型	300	450	600

按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆．
（Ⅰ）求z的值；
（Ⅱ）用分层抽样的方法在C类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；
（Ⅲ）用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分x的值如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2，把这8辆轿车的得分看成一个总体，从中任取一个数x_i（1≤i≤8，i∈N），设样本平均数为

，求|x_i﹣

|≤0.5的概率．

共享时间:2021-05-18 难度:2 相似度:2

解析

纠错

下载

组卷白板

237954. （2017•西安中学•高一下期中）在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个小球被取出的可能性相等．
（Ⅰ）求取出的两个球上标号为相邻整数的概率；
（Ⅱ）求取出的两个球上标号之和能被3整除的概率．

共享时间:2017-05-28 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

172439. （2021•西安中学•高二上期中）体育测试成绩分为四个等级，优、良、中、不及格．某班50名学生参校测试结果如下：

等级	优	良	中	不及格
人数	5	19	23	3

（1）从该班任意抽取1名学生，求该名学生的测试成绩为“良”或“中”的概率；
（2）测试成绩为“优”的3名男生记为a₁，a₂，a₃，2名女生的成绩记为b₁，b₂，现从这5人中任选2人参加学校的某项体育比赛：
①写出所有可能的基本事件；
②求参赛学生中恰有一名女生的概率．

共享时间:2021-11-29 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

166795. （2024•西安工业大学附中•高二上一月）某地教育研究中心为了调查该地师生对“高考使用全国统一命题的试卷”这一看法，对该市区部分师生进行调查，先将调查结果统计如下：

	赞成	反对	总计
教师	120
学生		40
总计	280	120

（1）请将表格补充完整，若该地区共有教师30000人，以频率为概率，试估计该地区教师反对“高考使用全国统一命题的试卷”这一看法的人数；
（2）按照分层抽样从“反对”的人中先抽取6人，再从中随机选出3人进行深入调研，求深入调研中恰有1名学生的概率．

共享时间:2024-10-20 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

236350. （2017•长安区一中•高二上期末）某旅游爱好者计划从3个亚洲国家A₁，A₂，A₃和3个欧洲国家B₁，B₂，B₃中选择2个国家去旅游．
（Ⅰ）若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；
（Ⅱ）若从亚洲国家和欧洲国家中各任选1个，求这2个国家包括A₁但不包括B₁的概率．

共享时间:2017-02-09 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

233207. （2023•长安区一中•高一下二月）设甲、乙、丙三个乒乓球协会的运动员人数分别为27、9、18，现用分层抽样的方法从三个协会中抽取6名运动员参加比赛．
（Ⅰ）求应从这三个协会中分别抽取的运动员人数；
（Ⅱ）现从这6名运动员中随机抽取2名参加双打比赛．
（1）列出所有可能的结果；
（2）求选到的两名运动员来自同一协会的概率．

共享时间:2023-06-23 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

231769. （2025•师大附中•高二下二月）某学校安排甲、乙、丙三个班级同时到学校礼堂参加联欢晚会，已知甲班艺术生占比8%，乙班艺术生占比6%，丙班艺术生占比5%．学生自由选择座位，先到者先选．甲、乙、丙三个班人数分别占总人数的

，

．若主持人随机从场下学生中选一人参与互动．
（1）求选到的学生是艺术生的概率；
（2）如果选到的学生是艺术生，判断其来自哪个班的可能性最大．

共享时间:2025-06-30 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

171260. （2024•师大附中•高二下期中）某学校安排甲、乙、丙三个班级同时到学校礼堂参加联欢晚会，已知甲班艺术生占比8%，乙班艺术生占比6%，丙班艺术生占比5%．学生自由选择座位，先到者先选．甲、乙、丙三个班人数分别占总人数的

，

共享时间:2024-05-17 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

230955. （2017•西工大附中•六模）某保险的基本保费为a（单位：元），继续购买该保险的投保人成为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

上年度出险次数	0	1	2	3	4	≥5
保费	0.85a	a	1.25a	1.5a	1.75a	2a

设该险种一续保人一年内出险次数与相应概率如下：

一年内出险次数	0	1	2	3	4	≥5
概率	0.30	0.15	0.20	0.20	0.10	0.05

（Ⅰ）求一续保人本年度的保费高于基本保费的概率；
（Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；
（Ⅲ）求续保人本年度的平均保费与基本保费的比值．

共享时间:2017-05-26 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

237828. （2018•铁一中学•高二下期中） PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米至75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．某市环保局从市区2016年全年每天的PM2.5监测数据中，随机抽取15天的数据作为样本，监测值如茎叶图所示：（十位为茎，个位为叶）
（1）从这15天的数据中任取3天的数据，求空气质量至少有一天达到一级的概率；
（2）以这15天的PM2.5日均值来估算一年的空气质量情况，则一年（按360天计算）中大致有多少天的空气质量达到一级．

共享时间:2018-05-28 难度:2 相似度:1

解析

纠错

下载

组卷白板

237227. （2021•师大附中•高二下期中）已知函数f（x）＝x²﹣ax+b．
（1）若a，b都是从集合{0，1，2，3}中任取的一个数，求函数f（x）有零点的概率；
（2）若a，b都是从区间[0，3]上任取的一个数，求f（1）＞0成立的概率．

共享时间:2021-05-11 难度:2 相似度:1

解析

纠错

下载

组卷白板

231812. （2025•雁塔二中•高二下一月） 2017年5月，来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”：高铁、扫码支付、共享单车和网购．为发展业务，某调研组对A，B两个公司的扫码支付准备从国内n（n∈N^*）个人口超过1000万的超大城市和8个人口低于100万的小城市随机抽取若干个进行统计，若一次抽取2个城市，全是小城市的概率为

．
（1）求n的值；
（2）若一次抽取4个城市，则：
①假设取出小城市的个数为X，求X的分布列；
②取出4个城市是同一类城市求全为超大城市的概率．

共享时间:2025-04-27 难度:2 相似度:1

解析

纠错

下载

组卷白板

231562. （2015•西安一中•二模）欣欣服装厂在2010年第一季度共生产A、B、C三种品牌的男女休闲服装2000件，如下表所示

品牌	A	B	C
女羽绒服	373	x	y
男羽绒服	377	370	z

现从这些服装中随机抽取一件进行检验，已知抽到品牌B女服装的概率是0.19．
（1）求x的值；
（2）现用分层抽样的方法在生产的这些服装中随机抽取48件进行检验，问应在品牌C中抽取多少件？
（3）已知y≥245，z≥245，求品牌C中生产的女服装比男服装多的概率．

共享时间:2015-03-25 难度:2 相似度:1

解析

纠错

下载

组卷白板

230978. （2017•高新一中•一模）某地区农科所为了选择更适应本地区种植的棉花品种，在该地区选择了5块土地，每块土地平均分成面积相等的两部分，分别种植甲、乙两个品种的棉花，收获时测得棉花的亩产量如图所示：
（Ⅰ）请问甲、乙两种棉花哪种亩产量更稳定，并说明理由；
（Ⅱ）求从种植甲种棉花的5块土地中任选2块土地，这两块土地的亩产量均超过种植甲种棉花的5块土地的总平均亩产量的概率．

共享时间:2017-03-08 难度:2 相似度:1

解析

纠错

下载

组卷白板

230840. （2019•高新一中•一模）某地区农科所为了选择更适应本地区种植的棉花品种，在该地区选择了5块土地，每块土地平均分成面积相等的两部分，分别种植甲、乙两个品种的棉花，收获时测得棉花的亩产量如图所示：
（Ⅰ）请问甲、乙两种棉花哪种亩产量更稳定，并说明理由；
（Ⅱ）求从种植甲种棉花的5块土地中任选2块土地，这两块土地的亩产量均超过种植甲种棉花的5块土地的总平均亩产量的概率．

共享时间:2019-03-06 难度:2 相似度:1

解析

纠错

下载

组卷白板

gw@dyw.com

2023-07-17

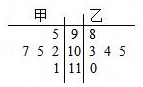
高中数学 | 高一下 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2022-2023学年陕西师大附中高一（下）期末数学试卷

更新:2023-07-17 07:37浏览量:20

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手