服务热线
搜题▪组卷
，0）对称
对称
]，则函数f（x）的值域为[﹣
，
]
，kπ+
]（k∈Z）
），
时，f（
）＝0，故A正确；
时，f（
）＝2sin（
）＝0，故B错误；
，故
，故．
，故C错误；
，整理得x∈[kπ+
，kπ+
]（k∈Z），函数f（x）的单调递减区间为[kπ+
，kπ+
]（k∈Z）故D正确．
A.函数y＝x﹣[x]在区间[k，k+1）（k∈Z）上单调递增
B.若函数
，则y＝[f（x）]的值域为{0}
C.．若函数
，则y＝[f（x）]的值域为{0，1}
D.x∈R，x≥[x]+1
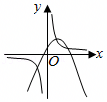
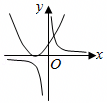
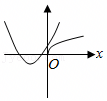
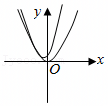
A.f（x）的单调减区间是（0，1），（1，e）
B.．f（x）的定义域是（0，1）∪（1，+∞）
C.．f（x）的值域是
D.．y＝m与y＝f（x）有一个公共点，则m＝e或m＜0
A.若f（x）的定义域为[﹣2，2]，则f（2x﹣1）的定义域为
B.函数
的值域为（﹣∞，2）∪（2，+∞）
C.函数
的值域为
D.函数f（x）＝x2﹣2x+4在[﹣2，2]上的值域为[4，12]
A.函数
的最大值为
B.已知函数y＝loga（2﹣ax）（a＞0且a≠1）在（0，1）上是减函数，则实数a的取值范围是（1，2）
C.函数y＝f（x）的定义域为[1，2]，则函数y＝f（2x）的定义域为[2，4]
D.若函数f（x）＝lg（ax2+5x+4）的值域为R，则实数a的取值范围是
A.方程f（g（x））＝0有且仅有6个根
B.．方程g（f（x））＝0有且仅有3个根
C.．方程f（f（x））＝0有且仅有4个根
D.方程g（g（x））＝0有且仅有4个根
A.f（x）的图像关于原点对称
B.f（x）的图像关于y轴对称
C.．f（x）的值域为（﹣1，1）
D.．∀x1，x2∈R，且
A.f（2019.67）＝0.67
B.．
C.方程
有无数个根
D.当1≤x＜2时，f（x）＝x﹣1
A.函数f（x）在区间（1，2）上单调递增
B.．函数y＝f（x）的图象关于直线x＝2对称
C.．若x1≠x2，但f（x1）＝f（x2），则x1+x2＝2
D.函数f（x）有且仅有两个零点
A.函数f（x）恒过定点（0，1）
B.函数f（x）的值域为[0，+∞）
C.．函数f（x）在区间[0，+∞）上单调递增
D.若直线y＝2a与函数f（x）的图像有两个公共点，则实数a的取值范围是（0，1）
A.f[f（
）]＝3
C.若f（x）＝﹣1，则x＝2或x＝﹣3
B.．f（x）＜2的解集为（﹣∞，0）∪（1，+∞）
D.．∀x∈R，a＞f（x），则a≥3
A.
的定义域是[﹣1，2）∪（2，+∞）
B.．若函数f（2x﹣1）的定义域为（﹣1，3]，则函数f（x）的定义域为（0，2]
C.．函数f（x）＝x2﹣x+2在[﹣2，1]的值域为[2，8]
D.若函数f（x）＝lg（ax2+x+2）的值域为R，则实数a的取值范围是
．
jbp@dyw.com
2024-02-14
高中数学 | 高一上 | 多选题
纠错
收藏
下载
相似
组卷
解析
