服务热线
搜题▪组卷
．
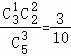，P（X＝2）＝
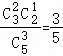，P（X＝3）＝
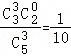，| X | 1 | 2 | 3 |
| P |  |
 |
 |
，
；
，＝
，
，
，且
，
}构成以
为首项，以
为公比的等比数列，
，
．
．| 等级 | 优 | 良 | 中 | 不及格 |
| 人数 | 5 | 19 | 23 | 3 |
| 时间 人数 学生类别 |
[0，5） | [5，10） | [10，15） | [15，20） | [20，25） | [25，30） | |
| 性别 | 男 | 6 | 9 | 10 | 10 | 9 | 4 |
| 女 | 5 | 12 | 13 | 8 | 6 | 8 | |
| 学段 | 初中 | x | 8 | 11 | 11 | 10 | 7 |
| 高中 | |||||||
，
，
．若主持人随机从场下学生中选一人参与互动．| 赞成 | 反对 | 总计 | |
| 教师 | 120 | ||
| 学生 | 40 | ||
| 总计 | 280 | 120 |
内有且仅有一个零点（记为xn）且
；
，
，E、F分别是BC、A1C1的中点．
| 检测结果 | 特等品 | 一等品 | 二等品 | 报废品 | |
| 甲公司 | 产品件数 | 210 | 54 | 20 | 16 |
| 乙公司 | 产品件数 | 240 | 18 | 28 | 14 |
| 每件特等品 | 每件一等品 | 每件二等品 | 报废品 | |
| 甲公司 | 盈2万元 | 盈1万元 | 亏1万元 | 亏2万元 |
| 乙公司 | 盈1.5万元 | 盈0.8万元 | 亏1万元 | 亏1.2万元 |
，数列{cn}的前n项和为Tn，且Tn＜m恒成立，求m的取值范围．| 调查的贫困户 | 支持以工代赈户数 | 支持整村推进户数 | 支持科技扶贫户数 | 支持移民搬迁户数 |
| 一般贫困户 | 1200 | 1600 | b | 200 |
| 五特户（五保户和特困户） | 100 | a | c | 100 |
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
，求|xi﹣
|≤0.5的概率．
dygzsxyn
2024-12-28
高中数学 | 高三上 | 解答题
纠错
收藏
下载
相似
组卷
解析