服务热线
搜题▪组卷
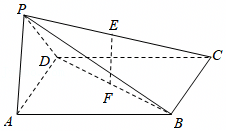
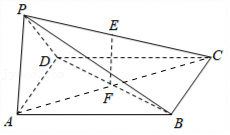
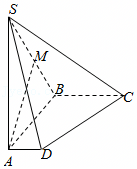
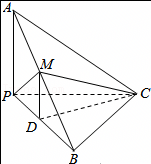
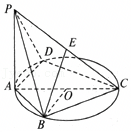
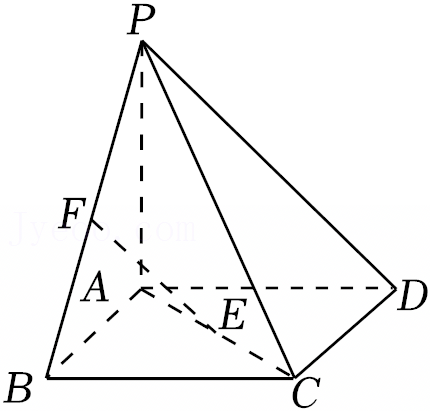
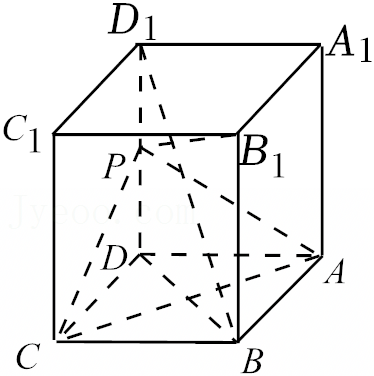

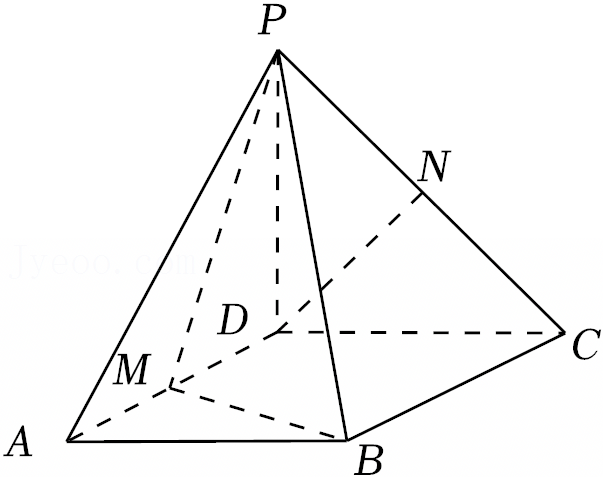
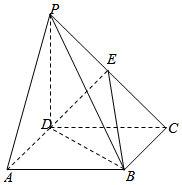 如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.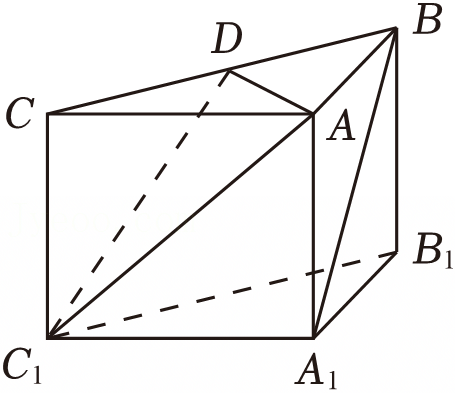



dygzsxyn
2023-10-22
高中数学 | 高二上 | 解答题