[考点]
全等三角形的判定与性质,平行四边形的判定与性质,
[答案]
(1)证明见解答;
(2)四边形AFCE周长是32.
[解析]
(1)证明:∵四边形ABCD为平行四边形,
∴OD=OB,
∵DE=BF,
∴OD+DE=OB+BF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形.
(2)解:∵AC平分∠EAF,
∴∠EAC=∠FAC,
∵四边形AFCE为平行四边形,OA=4,
∴CE∥AF,OC=OA=4,
∴∠ECA=∠FAC,AC=4+4=8,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AFCE是菱形,
∵∠AEC=60°,
∴△EAC是等边三角形,
∴AE=AC=8,
∴AF+CF+CE+AE=4AE=4×8=32,
∴四边形AFCE周长是32.
[点评]
本题考查了"全等三角形的判定与性质,平行四边形的判定与性质,",属于"必考题",熟悉题型是解题的关键。
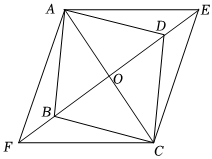 已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.
已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.