服务热线
搜题▪组卷
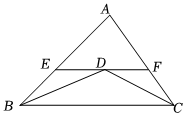 如图,在△ABC中,AB=8cm,AC=6cm,BD平分∠ABC,CD平分∠ACB,过点D作直线EF平行于BC,交AB,AC于点E,F.
如图,在△ABC中,AB=8cm,AC=6cm,BD平分∠ABC,CD平分∠ACB,过点D作直线EF平行于BC,交AB,AC于点E,F.
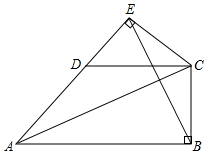
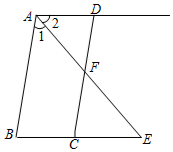 已知:如图,AD∥BC,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E,那么∠B与∠DCE相等吗?试说明理由.请将下面的推理过程补充完整.
已知:如图,AD∥BC,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E,那么∠B与∠DCE相等吗?试说明理由.请将下面的推理过程补充完整.

qbb@dyw.com
2024-04-24
初中数学 | 八年级下 | 解答题