服务热线
搜题▪组卷
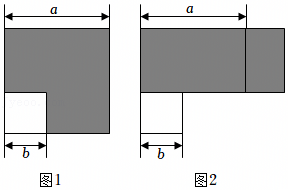
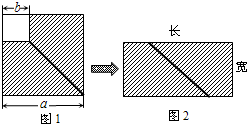 如图,边长为a的大正方形内有一个边长为b的小正方形.
如图,边长为a的大正方形内有一个边长为b的小正方形.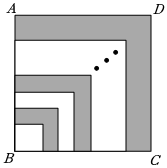 如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.
如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.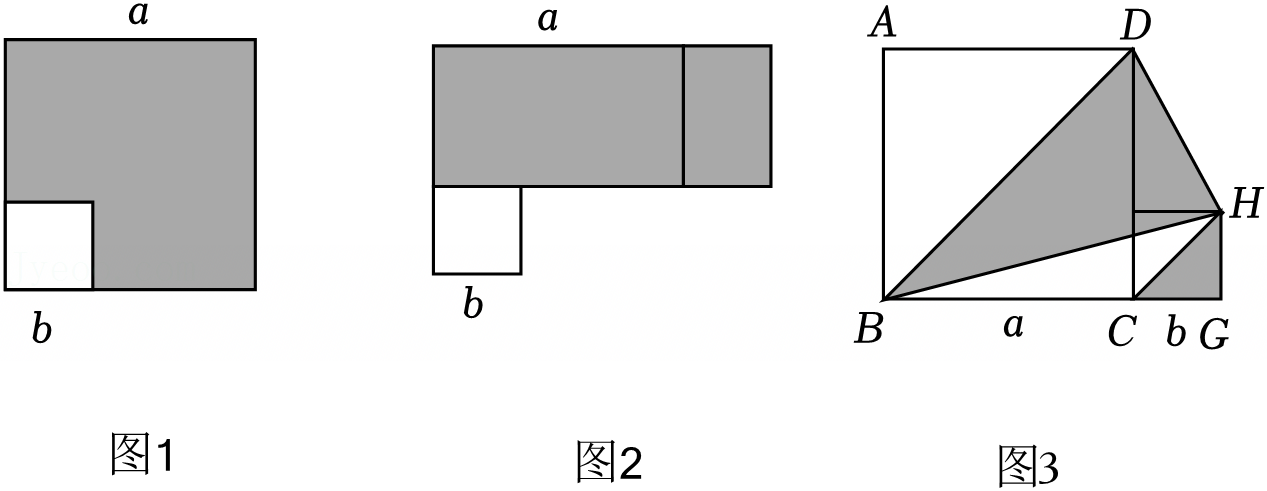

dyczsxyn
2024-05-28
初中数学 | 七年级下 | 解答题