已知是二次函数且求的表达式若任意恒成立试求实数的取值范围

首页 > 试题列表 > 单题解析

171695. （2023•西安八十五中•高一上期中）已知f（x）是二次函数，且f（0）＝1，f（x+1）﹣f（x）＝2x．
（1）求f（x）的表达式；
（2）若任意x∈[1，+∞），g（x）＝f（x）﹣a＞0恒成立，试求实数a的取值范围．

共享时间:2023-11-22 难度:3

纠错

下载

相似

组卷

[考点]

二次函数的性质与图象，函数解析式的求解及常用方法，函数恒成立问题，

[答案]

（1）f（x）＝x²﹣x+1；（2）（﹣∞，1）．

[解析]

解：（1）设f（x）＝ax²+bx+c，a≠0，
∵f（1）＝0，∴c＝1，∴f（x）＝ax²+bx+1，
f（x+1）＝ax²+（2a+b）x+a+b+1，
∴f（x+1）﹣f（x）＝2ax+a+b，
又f（x+1）﹣f（x）＝2x，
∴

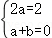，解得a＝1，b＝﹣1，
∴f（x）＝x²﹣x+1；
（2）由（1）知g（x）＝x²﹣x+1﹣a，
对任意x∈[1，+∞），g（x）＞0恒成立，
即a＜x²﹣x+1对任意x∈[1，+∞）恒成立．
∵y＝x²﹣x+1在x∈[1，+∞）单调递增，
∴当x＝1时，y的最小值为1，
∴a∈（﹣∞，1）．

[点评]

本题考查了"二次函数的性质与图象，函数解析式的求解及常用方法，函数恒成立问题，"，属于"难典题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

169897. （2023•长安区一中•高一上期末）已知函数f（x）＝x²﹣2bx+3，b∈R．
（1）若关于x的不等式f（x）＞0对一切实数x都成立，求b的取值范围；
（2）当x∈[﹣1，2]时，函数f（x）的最小值为1，求b值．

共享时间:2023-02-03 难度:2 相似度:1.67

解析

纠错

下载

组卷

171306. （2024•西安中学•高一上期中）已知f（x）是二次函数，且满足f（0）＝2，f（x+2）﹣f（x）＝2x+4．
（1）求f（x）的解析式；
（2）当x∈[m，m+1]，其中m∈R，求f（x）的最小值．

共享时间:2024-11-16 难度:2 相似度:1.67

解析

纠错

下载

组卷

170858. （2025•师大附中•高一下期中）已知函数f（x）＝x²﹣（a+6）x+6（a∈R）．
（1）若∀x∈[1，4]，f（x）+a+8≥0恒成立，求a的取值范围；
（2）已知g（x）＝mx+7﹣3m，当a＝1时，若对任意的x₁∈[1，4]，总存在x₂∈[1，4]，使f（x₁）＝g（x₂）成立，求实数m的取值范围．

共享时间:2025-05-01 难度:2 相似度:1.67

解析

纠错

下载

组卷

171827. （2022•西安中学•高一上期中）已知函数f（x）＝x²+ax．
（1）当x∈[﹣2，2]时，f（x）≥a恒成立，求实数a的取值范围；
（2）若对一切a∈[﹣3，3]，f（x）≥a﹣3恒成立，求实数x的取值范围．

共享时间:2022-11-28 难度:2 相似度:1.67

解析

纠错

下载

组卷

170991. （2024•庆安中学（高）•高一上期中）已知函数

，且f（1）＝10，f（3）＝6．
（1）求f（x）的解析式；
（2）判断f（x）在[3，+∞）上的单调性并用单调性的定义证明你的判断；
（3）若不等式f（m²+3）＞10恒成立，求m的取值范围．

共享时间:2024-11-30 难度:3 相似度:1.34

解析

纠错

下载

组卷

171125. （2024•西电附中•高一上期中）．已知函数

是定义在[﹣1，1]上的奇函数，且

．
（1）求a，b的值；
（2）求函数f（x）在[﹣1，1]上的值域；
（3）设g（x）＝kx+1﹣2k，若对任意的x₁∈[﹣1，1]，对任意的x₂∈[0，1]，使得f（x₁）≤g（x₂）成立，求实数k的取值范围．

共享时间:2024-11-21 难度:3 相似度:1.34

解析

纠错

下载

组卷

171417. （2023•长安区一中•高一上期中）已知f（x）＝ax²+x﹣a，a∈R．
（1）若不等式f（x）＞﹣2x²﹣3x+1﹣2a对一切实数x恒成立，求实数a的取值范围；
（2）若a＜0，解不等式f（x）＞1．

共享时间:2023-11-15 难度:3 相似度:1.34

解析

纠错

下载

组卷

171571. （2023•滨河中学•高一上期中）设二次函数f（x）满足f（1）＝﹣3，且关于x的不等式f（x）＜0的解集为（0，4）．
（1）求函数f（x）的解析式；
（2）若关于x的方程mf（x）﹣x+1＝0在区间（0，2）上有解，求实数m的取值范围．

共享时间:2023-11-16 难度:3 相似度:1.34

解析

纠错

下载

组卷

171762. （2022•师大附中•高一上期中）已知f（x）是定义在[﹣1，1]上的奇函数．当a，b∈[﹣1，1]，且a+b≠0时，有

成立．
（Ⅰ）判断函数f（x）的单调性，并证明；
（Ⅱ）若f（1）＝1，且f（x）≤m²﹣2bm+1对所有x∈[﹣1，1]，b∈[﹣1，1]恒成立，求实数m的取值范围．

共享时间:2022-11-26 难度:3 相似度:1.34

解析

纠错

下载

组卷

171696. （2023•西安八十五中•高一上期中）已知函数f（x）＝﹣4x²+4ax﹣4a﹣a²，求f（x）在区间[0，1]上的最小值．

共享时间:2023-11-22 难度:1 相似度:1.33

解析

纠错

下载

组卷

167391. （2023•高新一中•高一上一月）设f（x）＝ax²+（1﹣a）x+a﹣2．
（1）若不等式f（x）≥﹣2对于一切实数x恒成立，求实数a的取值范围；
（2）解关于x的不等式f（x）＜a﹣1（a∈R）．

共享时间:2023-10-22 难度:1 相似度:1.33

解析

纠错

下载

组卷

171200. （2024•西安八十九中•高一上期中）某学校为了支持生物课程基地研究植物生长，计划利用学校空地建造一间室内面积为900m²的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔1m，三块矩形区域的前、后与内墙各保留1m宽的通道，左、右两块矩形区域分别与相邻的左右内墙保留3m宽的通道，如图．设矩形温室的室内长为x（m），三块种植植物的矩形区域的总面积为S（m²）．
（1）求S关于x的函数关系式；
（2）求S的最大值，及此时长x的值．

共享时间:2024-11-19 难度:1 相似度:1.33

解析

纠错

下载

组卷

169234. （2025）若存在实数对（a，b），使等式f（x）•f（2a﹣x）＝b对定义域中每一个实数x都成立，则称函数f（x）为（a，b）型函数．
（1）若函数f（x）＝2^x是（a，1）型函数，求a的值；
（2）若函数

是（a，b）型函数，求a和b的值；
（3）已知函数h（x）定义在[﹣2，4]上，h（x）恒大于0，且为（1，4）型函数，当x∈（1，4]时，

．若h（x）≥1在[﹣2，4]恒成立，求实数m的取值范围．

共享时间:1970-01-01 难度:1 相似度:1.33

解析

纠错

下载

组卷

169462. （2024•长安区一中•高一上期末）已知函数

为奇函数．
（1）求实数a的值，并用定义证明函数f（x）的单调性；
（2）若对任意的t∈R，不等式f（t²+3）+f（t²﹣tk）＞0恒成立，求实数k的取值范围．

共享时间:2024-02-14 难度:1 相似度:1.33

解析

纠错

下载

组卷

170510. （2022•高新一中•高一上期末）若函数y＝f（x）对定义域内的每一个值x₁，在其定义域内都存在唯一的x₂，使得f（x₁）f（x₂）＝1成立，则称该函数为“依赖函数”．
（1）判断函数g（x）＝sinx是否为“依赖函数”，并说明理由；
（2）若函数f（x）＝2^x^﹣1在定义域[m，n]（m＞0）上为“依赖函数”，求mn的取值范围；
（3）已知函数h（x）＝（x﹣a）²