服务热线
试卷总分:120分 命题人:dyczsxyn 考试时长:120分钟
| A.流星划过夜空 | B.打开折扇 |
| C.汽车雨刷的转动 | D.旋转门的旋转 |
A.在-4表示的点的左边
B.在-2表示的点和原点之间
C.由1表示的点向左平移4个单位长度得到
D.和原点的距离是-3
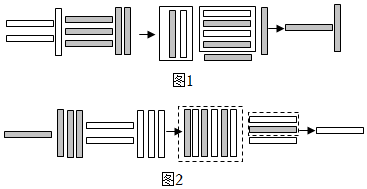
| A.（-13）+（+23）=10 | B.（-31）+（+32）=1 |
| C.（+13）+（+23）=36 | D.（+13）+（-23）=-10 |
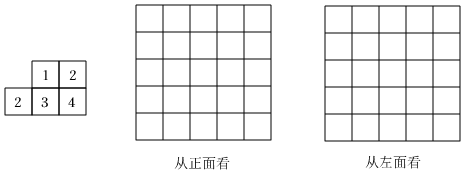
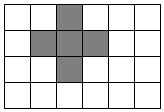小强用5个大小一样的正方形制成如图所示的拼接图形（阴影部分），若在图中只添加一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子，这样的拼接方式有 种．
，0，﹣3.14，5.9，﹣92．
πr2h）
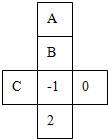如图是一个正方形盒的展开图，若在其中的三个正方形A、B、C、内分别填入适当的数，使得它们折成正方体后相对的面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为多少？
| 月份 | 一月份 | 二月份 | 三月份 | 四月份 | 五月份 | 六月份 |
| 甲厂 | -0.2 | -0.4 | +0.5 | 0 | +1.2 | +1.3 |
| 乙厂 | +1.0 | -0.7 | -1.5 | +1.8 | -1.8 | 0 |
如图，数轴上点A在原点的左侧，到原点的距离为3个单位长度，点B在点A的右侧，与点A的距离为5个单位长度，点A，B对应的数分别为a,b.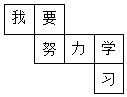
如图，是一个正方体的六个面的展开图形（字在外表面），回答下列问题：
dyczsxyn
2022-10-23
初中数学 | 考试 | 难度:1.85
平行组卷卷生成中,请等待
解析
纠错
收藏
下载
相似
组卷
如图所示的正方体，下列选项中哪一个图形是它的展开图（ ）
某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有（ ）
如图，将一个装了一半水的密闭圆柱形玻璃杯水平放置时，水面的形状是 ．
