德优网2025陕西省西安市高新区高新一中初中数学段考期中七年级上
2025-2026学年陕西省西安市雁塔区高新一中七年级(上)期中数学试卷
试卷总分:120分
命题人:cbem@dyw.com
考试时长:0分钟
一、选择题(8小题共24分)
1.
(本题3分)
﹣2025的相反数是( )
A.2025
B.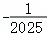
C.﹣2025
D.
2.
(本题3分)
用数学的眼光观察我们身边的物体,下列可以抽象为棱柱的物体是( )
3.
(本题3分)
2025年双节期间(9月30日至10月8日),西安地铁线网日均平安运送乘客430万人.数据430万用科学记数法表示为( )
A.4.3×105
B.4.3×106
C.0.43×107
D.43×105
4.
(本题3分)
下列说法中,正确的是( )
A.8πxy3的次数为5
B.多项式x3﹣2x2﹣5x的一次项是5x
C.单项式m没有系数
D.多项式x2+6x+18是二次三项式
5.
(本题3分)
若﹣8xmy3与x2yn的和是单项式,则m﹣n的值是( )
6.
(本题3分)
下列各组数中,相等的是( )
A.﹣23与(﹣2)3
B.﹣(﹣1)与﹣|﹣1|
C.a与|a|
D.(﹣3)2与﹣32
7.
(本题3分)
在如图所示的运算程序中,若开始输入的x值为4,我们发现第一次输出的结果为1( )
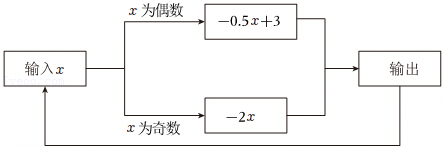
8.
(本题3分)
将“数学核心素养”六个字分别写在如图所示的正方体盒子的六个面上,将图1盒子在桌面上向右翻滚90°,接着按逆时针方向旋转90°.若把该正方体盒子打开( )

A.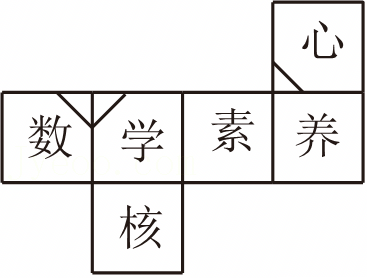
B.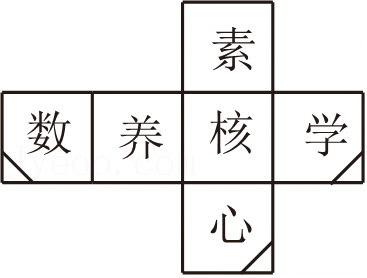
C.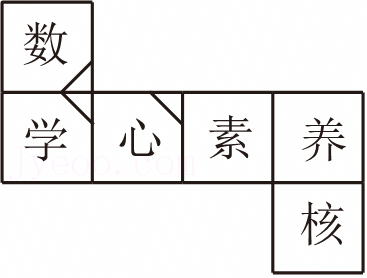
D.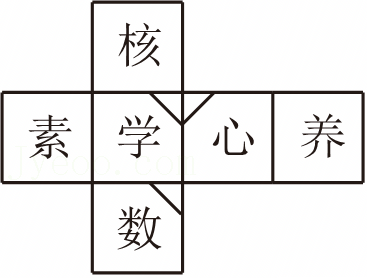
【考点】专题:正方体相对两个面上的文字;旋转的性质.菁优网版权所有
【答案】B
【解答】解:由向右翻滚90°前后所露出的面可知,“心”与“素”是对面,
由逆时针旋转90°前后所露出的面可知,“数”与“核”是对面,
于是“学”与“养”是对面,
A.由正方形表面展开图的“相间,“数”与“素”相对,因此选项A不符合题意;
B.由正方形表面展开图的“相间,“心”与“素”,“学”与“养”相对,因此选项B符合题意;
C.由正方形表面展开图的“相间,“心”与“养”相对,因此选项C不符合题意;
D.由正方形表面展开图的“相间,“心”与“素”,“学”与“养”相对,因此选项D不符合题意;
故选:B.
二、填空题(6小题共18分)
9.
(本题3分)
在标准大气压下,四种物质的熔点如表所示,其中熔点最低的物质是 .
| 物质 |
冰 |
乙醇 |
氮气 |
甘油 |
| 熔点(单位:℃) |
0 |
﹣114 |
210 |
18 |
10.
(本题3分)
在今年举行的纪念中国人民抗日战争暨世界反法西斯战争胜利80周年阅兵仪式中,空军八一飞行表演队飞过后留下的彩烟轨迹,以其精美的设计和深刻的寓意,这一现象用数学知识可解释为 .
11.
(本题3分)
小新同学发明了一种游戏,将0,﹣1,1,5,6,7,﹣8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等.他已经将﹣1,1,7这四个数填入了圆圈,则图中a+b的值为 .
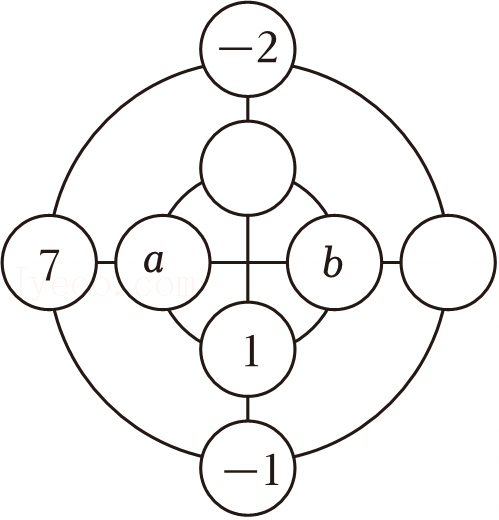
12.
(本题3分)
如图,有理数a,b,c,d在数轴上分别对应点A,B,C,则ab 0.
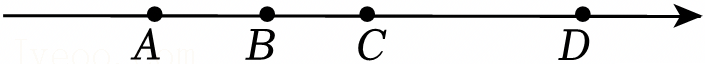
13.
(本题3分)
“CT检查”的原理是通过扫描和计算,把人体从不同角度“切”成无数薄层,每一层就是一个截面图象,如图1所示.为探明其内部构造,我们可以给这个物体做“CT检查”,得到一组自左向右的截面(如图2),则这个物体的内部构造可能为一个 体.

14.
(本题3分)
当n为非零整数时,代数式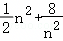 的最小值是 .
的最小值是 .
三、解答题(9小题共78分)
15.
(本题12分)
计算:
(1)(+12)﹣5+(﹣12)﹣(﹣39);
(2)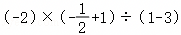 ;
(3)
;
(3)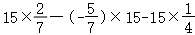 ;
(4)﹣12026×2+24÷4+|﹣3|.
;
(4)﹣12026×2+24÷4+|﹣3|.
16.
(本题8分)
(1)化简:1﹣3x2+10x+2x2+5x;
(2)先化简,再求值:﹣3(a2﹣2ab)+2(﹣5ab﹣4a2),其中a=﹣1,b=2.
17.
(本题6分)
如图是由五个大小相同的正方体搭成的几何体,请画出从正面和从左面看到的这个几何体的形状图.

18.
(本题6分)
智慧机器犬,也称为“四足机器人”或“仿生机器人”,是一种模仿犬类生物形态和运动方式的智能机器人.它是集成了人工智能、先进传感、仿生控制和5G通信等前沿技术的尖端装备,它每天都会在小区的一条东西方向主干道上例行巡逻.规定充电桩位置为起点,充电桩以东为正方向(单位:km)记录如下:+1.6,﹣1.2,﹣0.8,+1.8,+2.3,﹣2.
(1)该机器犬当天巡逻结束后是否返回充电桩?请通过计算说明;
(2)若机器犬每巡逻1km耗电0.1千瓦时,请求出该机器犬当日巡逻耗电多少千瓦时?
19.
(本题8分)
现有4张写着不同数字的卡片,利用所学过的加、减、乘、除、乘方运算按要求解答下列问题(每张卡片上的数字只能用一次):
(1)从中取出2张卡片,使这2张卡片上数字的积最大,则积的最大值是 ;从中取出2张卡片,使这2张卡片上数字的商最小,则商的最小值是 ;
(2)从中取出2张卡片,使这两张卡片上的数字经过一次运算后得到的结果最大,你所选择的数字是 ,结果的最大值是 ;
(3)用这4张卡片上的数字写出一个结果为24或﹣24的算式.(写出一个符合要求的即可)

20.
(本题8分)
某数学兴趣小组开展综合实践活动,活动的任务是制作收纳盒,该小组给出了两种设计
(1)利用图1所示的图形,制作的收纳盒形状为 ;
(2)哪一种收纳盒的容积更大?请根据图中所给信息计算说明.

21.
(本题8分)
为了鼓励公民节约用水,某市制定了居民用水“阶梯式水价”收费标准,具体如下:
| 计费档 |
户年用水量/m3 |
单价/(元/m3) |
| 第一档 |
不超过144m3 |
3.8 |
| 第二档 |
超过144m3但不超过207m3 |
6.1 |
| 第三档 |
超过207m3 |
8.4 |
(1)某户一年用水量是100m3,则该户这一年的水费是 元;
(2)某户一年用水量是xm3(144m3<x≤207m3)时,则该户这一年的水费是 元(用含x的代数式表示);
(3)某户去年一年的水费是913.2元,求该户去年一年的用水量.
23.
(本题12分)
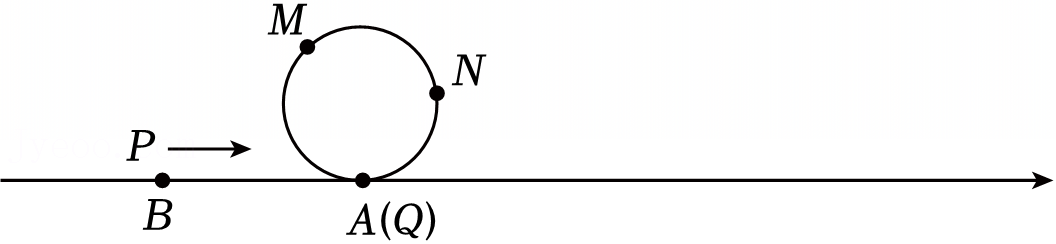
如图所示,点A,B,C是数轴上三点,B分别表示有理数a,b,且(a﹣2)2+|b+6|=0,点C表示20.现有一圆从点A出发以2个单位长度/s的速度沿数轴按顺时针方向滚动(圆与数轴的接触点为圆的最低点),动点P从点B出发以4个单位长度/s的速度沿数轴向右运动.已知圆的周长为6个单位长度,N和Q分别是圆的三等分点,开始时
(1)点A表示数 ,点B表示数 ,当圆滚动5s时,圆的最低点在数轴上对应的数为 ;
(2)若点P在圆滚动5s后开始运动,当P到达数轴上38对应的点时,立刻以原速返回(向左运动),它与圆的最低点重合?并通过计算说明此时点M,N,Q是否与点P重合.
(3)动点K从点C出发以3个单位长度/s的速度沿数轴向左运动,点P和圆分别从点B,A同时出发.若点P到圆的最低点间的距离记为m,P间的距离记为n,则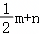 的最小值是多少?请直接写出答案.
的最小值是多少?请直接写出答案.
转载声明:
本题解析属于发布者收集录入,如涉及版权请向平台申诉!
!版权申诉