服务热线
搜题▪组卷
的菱形ABCD的对角线，∠ABC＝60°．点M和N分别从点B、C同时出发，以相同的速度沿BC、CA向终点C和A运动．连接AM和BN，交于点P．求△APB周长的最大值．
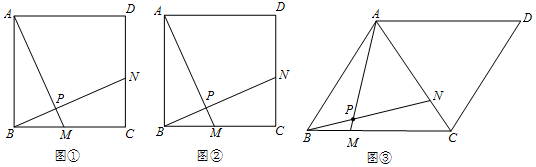
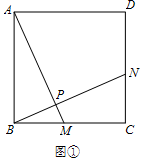∵四边形ABCD是正方形，
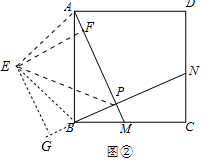∵∠EFP＝∠FPG＝∠G＝90°，
，
．
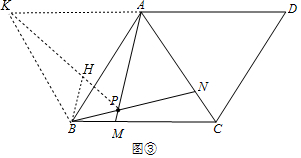∵AB＝BC，∠ABM＝∠BCN，BM＝CN，
+4．
如图，在Rt△ABC中，∠ACB=90°，AC=BC=4，CD⊥AB于D，将线段CD绕点C顺时针旋转90°得到CF，连接AF交CD于点G．
，CD＝1，求FE的长．
△ACB为等腰直角三角形，∠ACB=90°，点D为边AB上一点，以CD为边作等腰直角三角形DCE，且∠DCE=90°，连接BE，若AD=4，BD=10，求△BDE的面积．
如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，求证：
已知：如图，△ABC为等边三角形，AE=BD，AD，CE相交于点F．
gxyz515
2017-06-23
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE=DF=2，BE与AF相交于点G，点H为BF的中点，连接GH，求GH的长．
如图，在△ABC中，∠BAC=90°，AB=AC=2，点D是边BC上一点，E是边AC上一点，∠ADE=45°，BD=CE．求∠ADB的度数．
Rt△ABC中，∠C=90°，过点A作AE⊥AC，且AE=AC，过点E作ED⊥AB分别交AB、AC于点F、D，若BC=3，AE=7，求CD的长．
已知：如图等边三角形ABC中，D是AC中点，过C作CE∥AB，且AE⊥CE，求证：BD=AE．
如图，在△ABC中，∠BAC=90°，AC=AB，BE⊥AD于点E，CD⊥AD于点D，连接BD．若CD=7，DE=17，求AB．
如图，已知三角形ABC，∠ACB=90°，AC=BC，在AB上求作一点D，使得AD=CD．（尺规作图，不写作法，保留作图痕迹）
