服务热线
搜题▪组卷
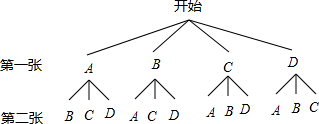

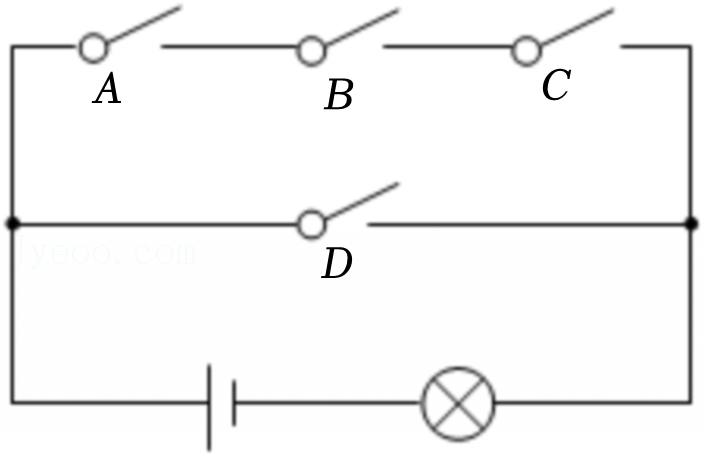
 随着高铁、地铁的大量兴建以及铁路的改扩建,我国人民的出行方式越来越多,出行越来越便捷.为保障旅客快捷、安全的出入车站,每个车站都修建了如图所示的出入闸口.某车站有四个出人闸口,分别记为A、B、C、D.当甲乙两名乘客通过该站闸口时,请用树状图或列表法求甲乙两名乘客选择相同闸口通过的概率.
随着高铁、地铁的大量兴建以及铁路的改扩建,我国人民的出行方式越来越多,出行越来越便捷.为保障旅客快捷、安全的出入车站,每个车站都修建了如图所示的出入闸口.某车站有四个出人闸口,分别记为A、B、C、D.当甲乙两名乘客通过该站闸口时,请用树状图或列表法求甲乙两名乘客选择相同闸口通过的概率.

tyz511
2019-05-31
初中数学 | | 解答题