问题发现如图将置于平面直角坐标系中直角顶点与原点重合点落在轴上点落在轴上已知是轴上一点将沿折叠使点落在边上的点处则点的坐标为问题探究如图将长方形置于平面直角坐标系中点在轴上点在轴上已知是上一点将长方形沿折叠点恰好落在对角线上的点处求所在直线的函数表达式如图将长方形置于平面直角坐

首页 > 试题列表 > 单题解析

23184. （2021•西工大附中•八上期中）【问题发现】
（1）如图①，将Rt△AOB置于平面直角坐标系中，直角顶点O与原点重合，点A落在x轴上，点B落在y轴上，已知A（4，0），B（0，3），C是x轴上一点，将Rt△AOB沿BC折叠，使点O落在AB边上的点D处，则点C的坐标为．
【问题探究】
（2）如图②，将长方形OABC置于平面直角坐标系中，点A在y轴上，点C在x轴上，已知B（12，5），E是OA上一点，将长方形OABC沿CE折叠，点O恰好落在对角线AC上的点F处，求OF所在直线的函数表达式．
（3）如图③，将长方形OABC置于平面直角坐标系中，点A在y轴上，点C在x轴上，已知B（8，6），D在对角线AC上，且CD=OC，P是OD的中点，Q是OC上一点，将△OPQ沿PQ折叠，使点O落在AC边上的点E处，求点D的坐标及四边形OPEQ的面积．
$德优题库$

共享时间:2021-11-19 难度:5

纠错

下载

相似

组卷白板

[考点]

一次函数的性质，待定系数法求一次函数解析式，一次函数综合应用，勾股定理，四边形与面积问题，翻折变换（折叠问题），

[答案]

（1）（，0）；（2）y=5x；（3）D（1.6，4.8），9.6．

[解析]

解：（1）设OC为x，
∵A（4，0），B（0，3），
∴AB＝

＝

＝5，
由翻折可知，DB＝OB＝3，OC＝CD＝x，
∴AD＝2，
由勾股定理得，AD²+CD²＝AC²，
即x²+2²＝（4﹣x）²，
解得x＝

，
∴点C的坐标为（

，0），
故答案为：（

，0）；
（2）∵长方形OABC，点A在y轴上，点C在x轴上，B（12，5），
∴A（0，5），C（12，0），
设直线AC的解析式为y＝kx+b，把A点和C点坐标代入得，

，
解得

，
∴直线AC的解析式为y＝﹣x+5，
由翻折可知，OC＝CF＝12，AF＝1，
设OE＝EF＝y，
由勾股定理得，EF²+AF²＝AE²，
即y²+1²＝（5﹣y）²，
解得y＝2.4，
即OE＝EF＝2.4，
∴AE＝2.6，
设点F的坐标为（m，﹣

m+5），
∴

×AF•EF＝

AE•x_F，
即

×1×2.4＝

×2.6m，
解得m＝

，
则点F的坐标为（

，

），
设直线OF的解析式为y＝dx，代入F点坐标得，

＝

d，
解得d＝5，
∴直线OF的解析式为y＝5x；
（3）连接OE，

∵P是OD的中点，
∴OP＝PD，
由折叠可知，OP＝PD＝PE，OE⊥PQ，
∴∠POE＝∠PEO，∠PED＝∠PDE，
∴∠PEO+∠PED＝90°，
∴OE⊥CD，
∴PQ∥CD，
∴Q是OC的中点，
∴三角形OPQ的面积是三角形OCD面积的四分之一，四边形OPEQ的面积是三角形OCD面积的二分之一，
∵B（8，6），
∴A（0，6），C（8，0），
∴AC＝

＝

＝10，
∴

OA•OC＝

AC•OE，
即

×6×8＝

×10×OE，
解得OE＝4.8，
∵OC＝CD＝8，
∴三角形OCD的面积为：

CD•OE＝

×8×4.8＝19.2，
∴四边形OPEQ的面积是

×19.2＝9.6，
∵三角形OCD的面积为19.2，OC＝8，
∴点D的纵坐标为19.2×2÷8＝4.8，
设直线AC的解析式为y＝nx+e，把A点和C点坐标代入得，

，
解得

，
∴直线AC的解析式为y＝﹣

x+6，
∵点D在直线AC上，当y＝4.8时，4.8＝﹣

x+6，
解得x＝1.6，
∴点D的坐标为（1.6，4.8）．

[点评]

本题考查了"一次函数的性质,待定系数法求一次函数解析式,一次函数综合应用,勾股定理,四边形与面积问题,翻折变换（折叠问题）"，属于"综合题"，熟悉考点和题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

2893. （2019•益新中学•模拟）为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：

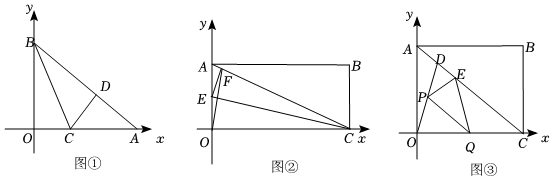
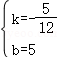车型	目的地
	A村（元/辆）	B村（元/辆）
	A村（元/辆）	大货车
	800	900
小货车	400	600

（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．

共享时间:2019-05-28 难度:3 相似度:1.17

解析

纠错

下载

组卷白板

93. （2020•上海•月考）如图，直线l₁：y＝2x+4与x轴交于点A，与y轴交于点B，直线l₂：y＝﹣x+2与y轴交于点C．
（1）直接写出点A、B、C的坐标分别为：A　　，B　　，C　　；
（2）是否存在将直线l₂：y＝﹣x+2向上或向下平移使其经过点D，且使得以A、B、C、D为顶点的四边形为平行四边形？若存在，求出所有可能的平移方式；若不存在，请说明理由．

共享时间:2021-01-06 难度:3 相似度:0.83

解析

纠错

下载

组卷白板

19059. （2015•交大附中•真题）荆州素有“鱼米之乡”的美称，某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售，按计划20辆汽车都要装运，每辆汽车只能装运同一种鱼，且必须装满，根据下表提供的信息，解答以下问题：

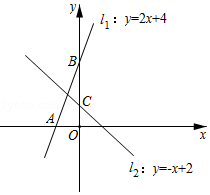
	鲢鱼	草鱼	青鱼
每辆汽车载鱼量（吨）	8	6	5
每吨鱼获利（万元）	0.25	0.3	0.2

（1）设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，求y与x之间的函数关系式；
（2）如果装运每种鱼的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．

共享时间:2016-06-21 难度:3 相似度:0.83

解析

纠错

下载

组卷白板

3145. （2018•滨河中学•真题）如果三角形的两个内角α与β满足2α+β＝90°，那么我们称这样的三角形为“准互余三角形”．
（1）若△ABC是“准互余三角形”，∠C＞90°，∠A＝60°，则∠B＝　　°；
（2）如图①，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．
（3）如图②，在四边形ABCD中，AB＝7，CD＝12，BD⊥CD，∠ABD＝2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

共享时间:2019-05-31 难度:5 相似度:0.83

解析

纠错

下载

组卷白板

6245. （2017•铁一中学•模拟）如图①，在 Rt△ABC中，AB＝4，BC＝3，将△ABC绕点B顺时针旋转α（0＜α＜120°）得△DBE，连接AD，EC，直线AD、EC交于点M．
（1）当α＝30°时，∠BAD＝　　．
（2）在旋转的过程中，四边形ABCM的面积是否存在最大值？若存在，求出四边形ABCM面积的最大值；若不存在，请说明理由；
（3）如图②，若△ABC中，∠ABC＝120°，其余条件不变，四边形ABCM的面积是否存在最大值？若存在，求出四边形ABCM面积的最大值；若不存在，请说明理由．

共享时间:2017-07-03 难度:5 相似度:0.73

解析

纠错

下载

组卷白板

6341. （2017•师大附中•模拟）我省某市为了缓解雾霾天气带来的危害，市绿化管理处派出洒水车为全市主干道进行洒水，以减缓雾霾天气对市民健康和出行带来的影响，每天的洒水量与投入的成本相应数据如下表：

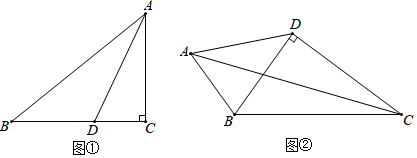
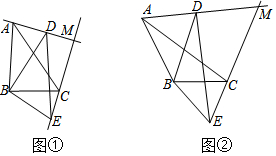
洒水量x（千克）	…	5000	6000	8000	10000	…
成本y（元）	…	300	324	372	420	…

（1）对上表中的数据分析探究后，发现投入的成本y（元）是洒水量x（千克）的一次函数，请你求出这个一次函数的关系式（不必写出自变量的取值范围）．
（2）由于近期雾霾严重，某天的洒水量是24000千克，则当天投入的成本是多少元？

共享时间:2017-06-08 难度:3 相似度:0.67

解析

纠错

下载

组卷白板

2895. （2019•益新中学•模拟）如图，PB为⊙O的切线，B为切点．过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
（1）求证：PA是⊙O的切线．
（2）若

，且OC＝4，求PA的长．

共享时间:2019-05-28 难度:3 相似度:0.67

解析

纠错

下载

组卷白板

21108. （2021•交大附中•九模）为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：

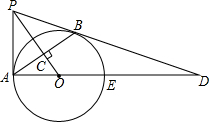
每月用气量	单价（元/m³）
不超出75m³的部分	2.5
超出75m³不超出125m³的部分	2.75
超出125m³的部分	3

（1）若调价后每月支出的燃气费为y（元），每月的用气量为x（m³），y与x之间的关系如图所示，求线段AB所表示的y与x之间的函数关系式；
（2）在（1）的条件下，若乙用户3月份用气80m³，应缴费多少元？

共享时间:2021-08-10 难度:3 相似度:0.67

解析

纠错

下载

组卷白板

21716. （2021•交大附中•七模）问题提出
（1）如图①，在等腰Rt△ABC中，∠ACB=90°，D是AB边上一点，以CD为腰作等腰Rt△CDE，连接BE，则AD与BE的数量关系是，位置关系是；
$德优题库$
问题探究
（2）如图②，AB是半圆O的直径，C、D是半圆O上两点，且AC=BC，若BD=3，AD=9，求CD的长；
问题解决
（3）如图③是某公园的一个面积为36π m²的圆形广场示意图，点O为圆心，公园开发部门计划在该广场内设计一个四边形运动区域ABDC，连接BC、AD，其中等边△ABC为球类运动区域，△BCD为散步区域，设AD的长为x，△BDC的面积为S．
①求S与x之间的函数关系式；
②按照设计要求，发现当点D为

的中点时，布局设计最佳，求此时四边形运动区域ABDC的面积．

共享时间:2021-07-25 难度:5 相似度:0.66

解析

纠错

下载

组卷白板

3143. （2018•滨河中学•真题）如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连接AD．已知∠CAD＝∠B．
（1）求证：AD是⊙O的切线．
（2）若BC＝8，tanB＝

，求⊙O的半径．
$德优题库$

共享时间:2019-05-31 难度:3 相似度:0.5

解析

纠错

下载

组卷白板

19118. （2016•益新中学•模拟）某蔬菜生产基地经市场调查，对种植的A、B、C三种蔬菜的成本与售价情况统计如表：

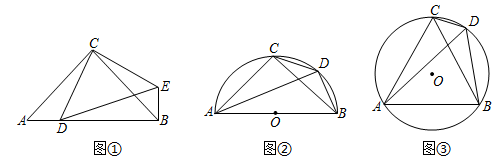
蔬菜品种	A	B	C
成本（元/吨）	3000	2200	1500
售价（元/吨）	7000	4000	3200

并且从市场调研中总结得知：该基地的蔬菜C的种植面积一般是蔬菜B种植面积的2倍，生产基地要按照这个规律种植，才不至于滞销．现知道基地共有用地200亩，蔬菜A每亩产量为3吨，蔬菜B每亩产量为5吨，蔬菜C每亩产量为7吨．若设种植蔬菜B为x亩，基地假设把生产的蔬菜都能销售出去，其利润为y元．
（1）求y与x之间的函数关系式；
（2）根据市场行情，蔬菜A的种植不能多于50亩，求该蔬菜生产基地在这次种植中能获得的最大利润．

共享时间:2016-06-20 难度:3 相似度:0.5

解析

纠错

下载

组卷白板

20161. （2021•西工大附中•四模）问题提出
（1）如图①，在矩形ABCD中，点E为AD边上一点，若S_△BCE＝4．则矩形ABCD的面积为______．
问题探究
（2）如图②，在△ABC中，∠BAC＝60°，BC边上的中线，AD＝6，求△ABC面积的最大值．
问题解决
（3）为迎接十四运，园林设计部门准备在奥体广场用鲜花拼成一个平行四边形的花卉展览场地供市民观赏．如图③所示，在平行四边形ABCD中，点E为AD边上一点且DE＝3AE，∠BEC＝60°，AB＝6米．为了种植更多的鲜花，要求四边形ABCD的面积尽可能大．请问四边形ABCD面积是否存在最大值？如果存在，请计算四边形ABCD面积的最大值；如果不存在，请说明理由．

共享时间:2021-05-31 难度:5 相似度:0.5

解析

纠错

下载

组卷白板

807. （2015•陕西省•真题）如图，AB是⊙O的直径，AC是⊙O的弦，过点B作⊙O的切线DE，与AC的延长线交于点D，作AE⊥AC交DE于点E．
（1）求证：∠BAD=∠E；
（2）若⊙O的半径为5，AC=8，求BE的长．

共享时间:2015-08-18 难度:3 相似度:0.5

解析

纠错

下载

组卷白板

20184. （2021•西工大附中•五模）如图，在△ABC中，AB＝AC，AE平分∠BAC，∠ABC的平分线BM
交AE于点M，点O在AB上，以点O为圆心，OB长为半径的圆经过点M，交BC于点G，交AB于点F．
（1）求证：AE为⊙O的切线．
（2）若BC＝8，AC＝12时，求BM的长．

共享时间:2021-06-03 难度:4 相似度:0.42

解析

纠错

下载

组卷白板

1143. （2020•陕西省•副题）如图，直线AM与⊙O相切于点A，弦BC∥AM，连接BO并延长，交⊙O于点E，交AM于点F，连接CE并延长，交AM于点D．
（1）求证：CE∥OA；
（2）若⊙O的半径R=13，BC=24，求AF的长．
$德优题库$

共享时间:2020-07-31 难度:4 相似度:0.42

解析

纠错

下载

组卷白板

dycs2021

2021-11-19

初中数学 | 八年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2021-2022学年陕西省西安市西工大附中八上数学期中试卷

更新:2021-11-19 03:19浏览量:1213

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手