服务热线
搜题▪组卷
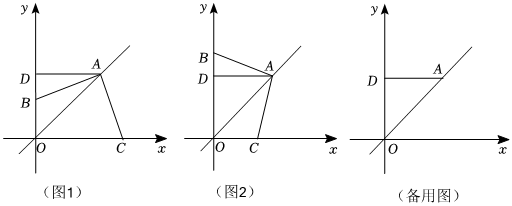
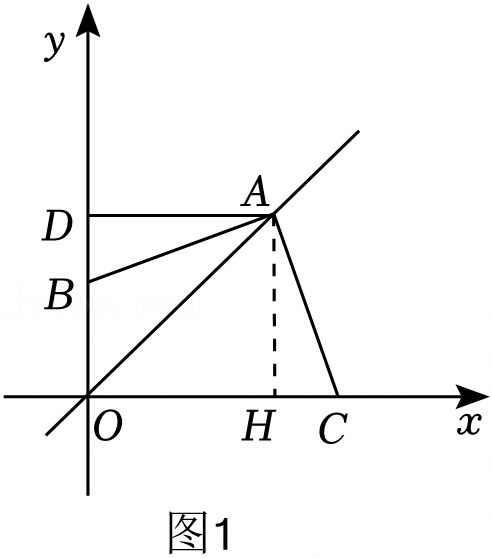
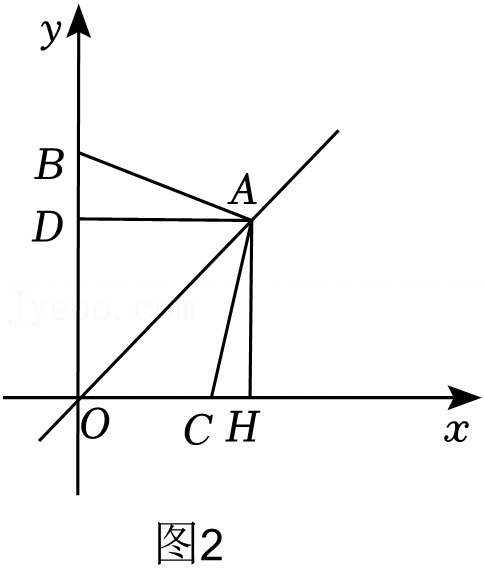
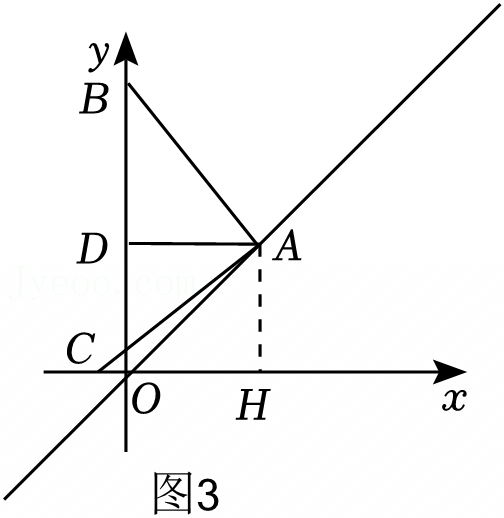
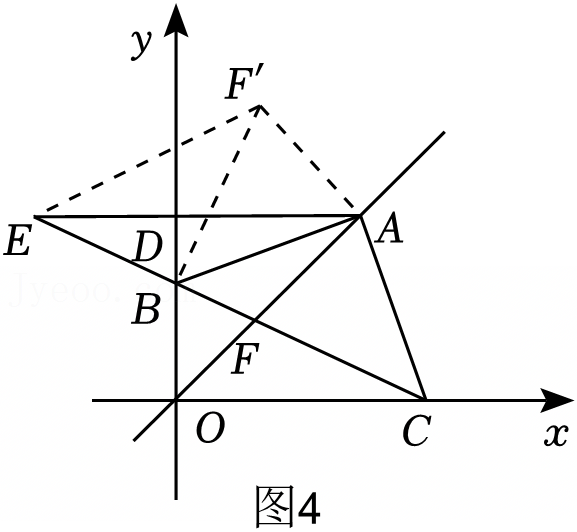

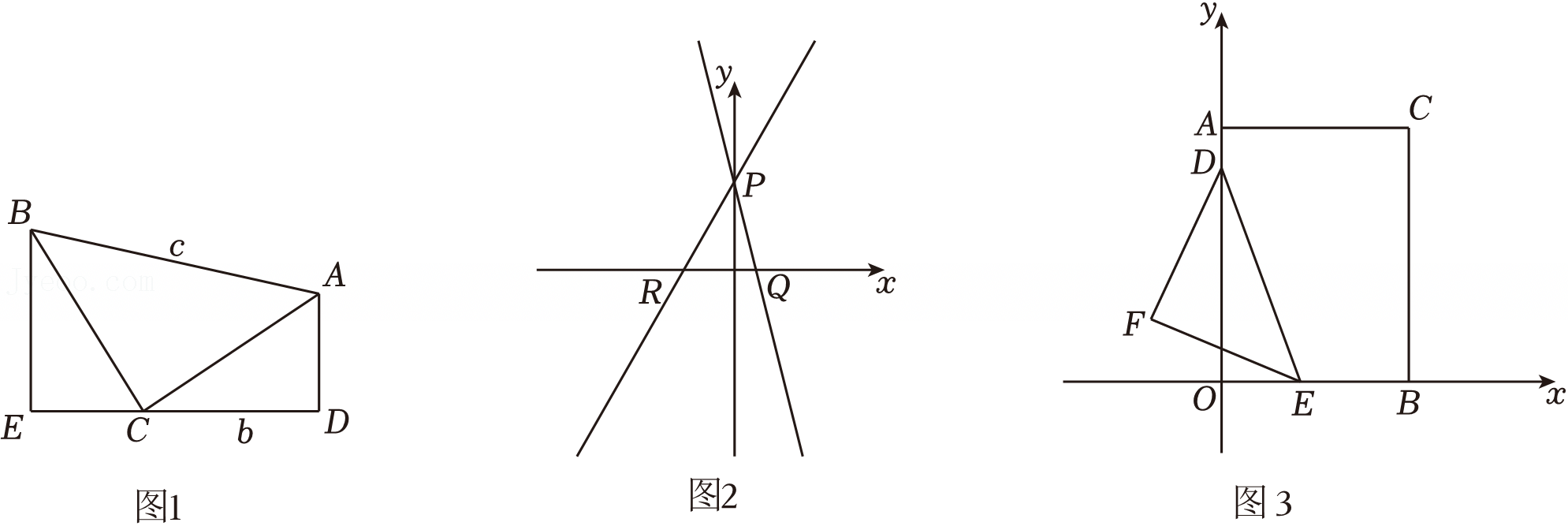
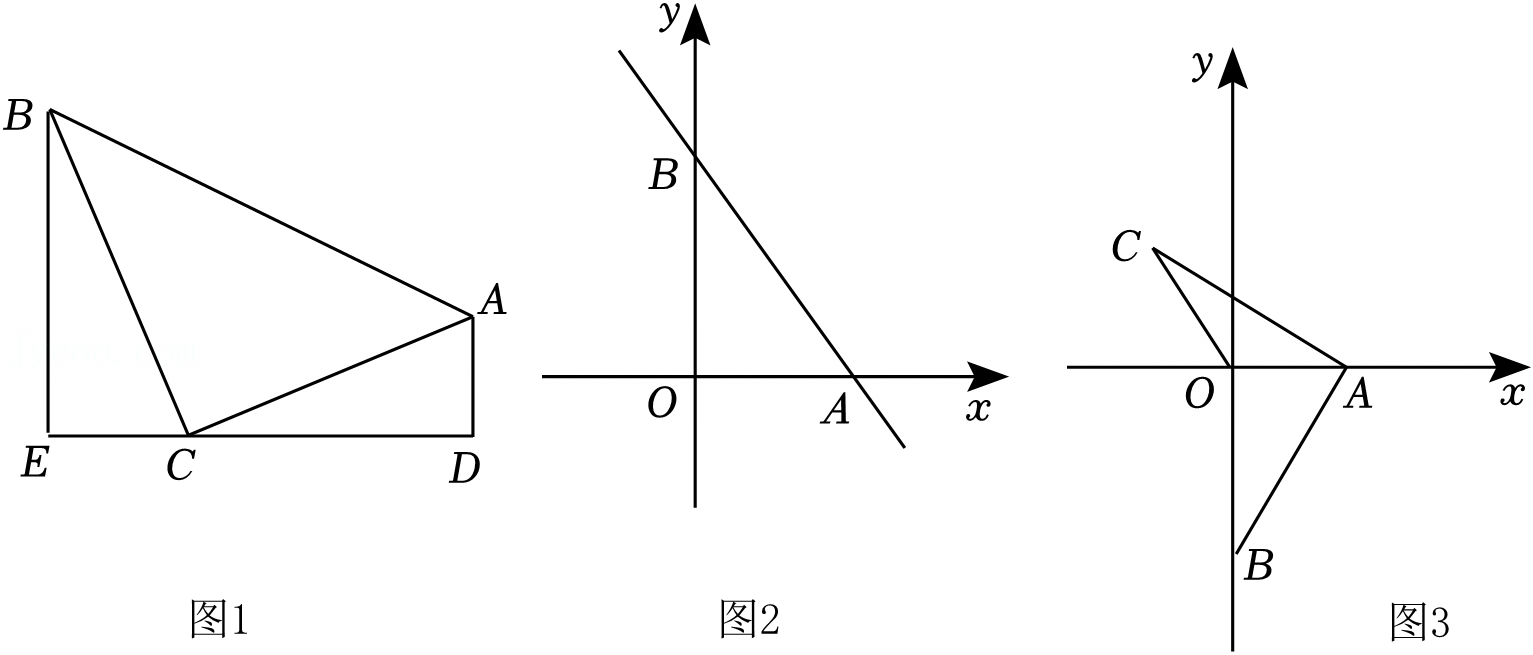
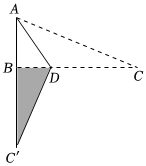 如图所示,在△ABC中,AB=5,BC=12,AC=13,把△ABC沿AD折叠,使AC落在直线AB上.
如图所示,在△ABC中,AB=5,BC=12,AC=13,把△ABC沿AD折叠,使AC落在直线AB上.
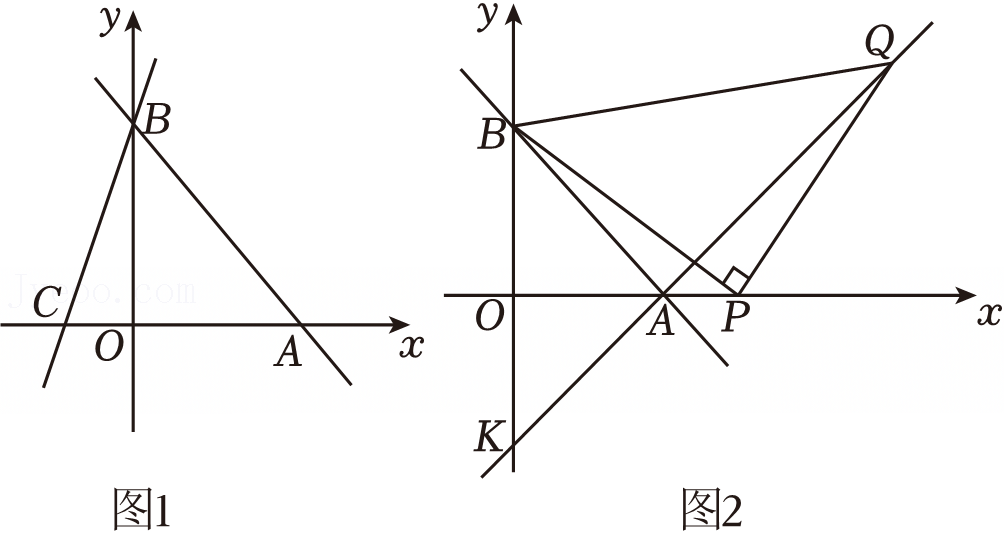
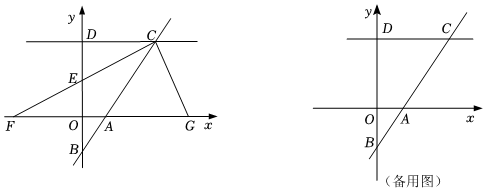
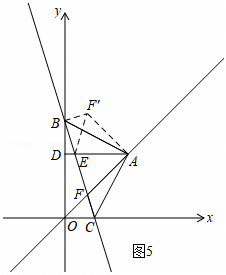
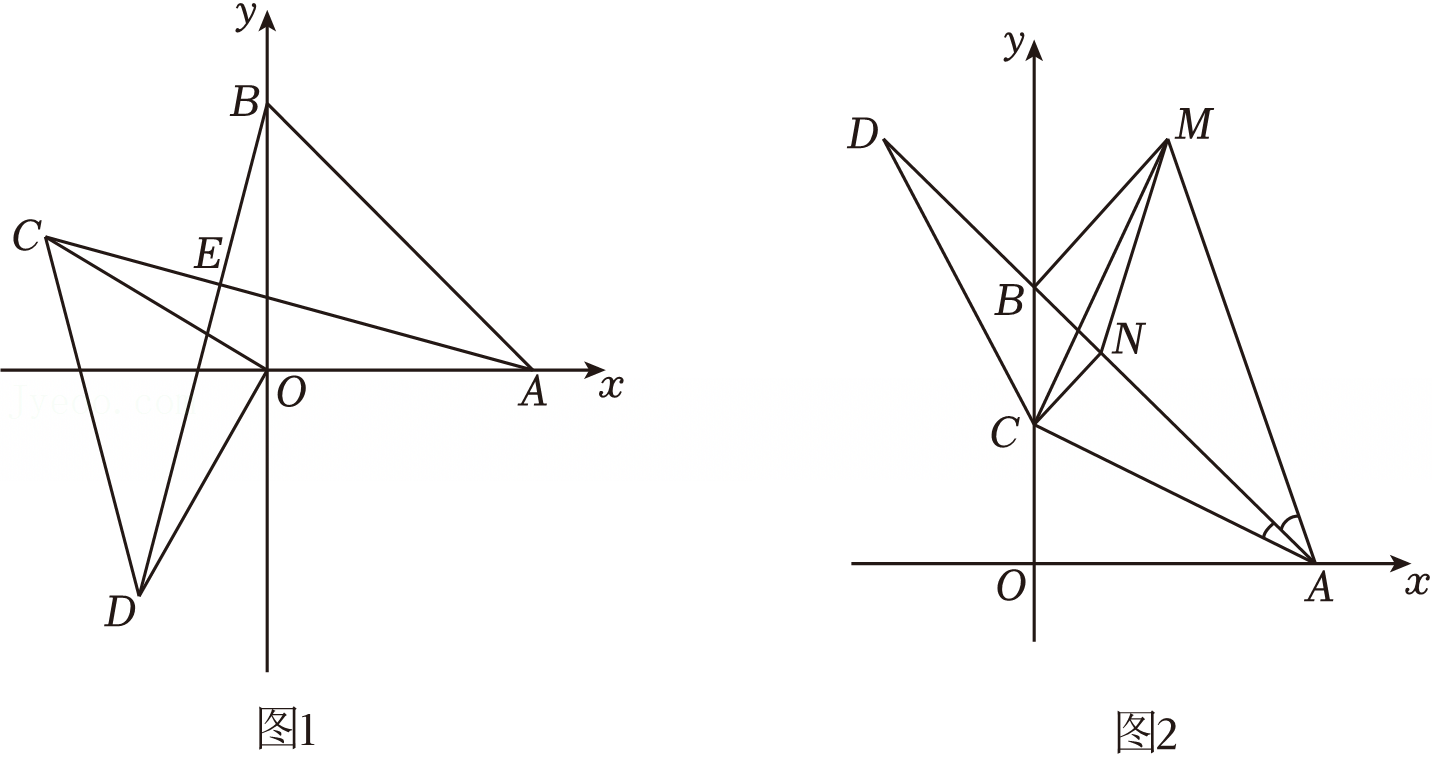
 如图,在平面直角坐标系中,直线AB分别交y轴,x轴于A(0,3),B(-9,0)两点.
如图,在平面直角坐标系中,直线AB分别交y轴,x轴于A(0,3),B(-9,0)两点.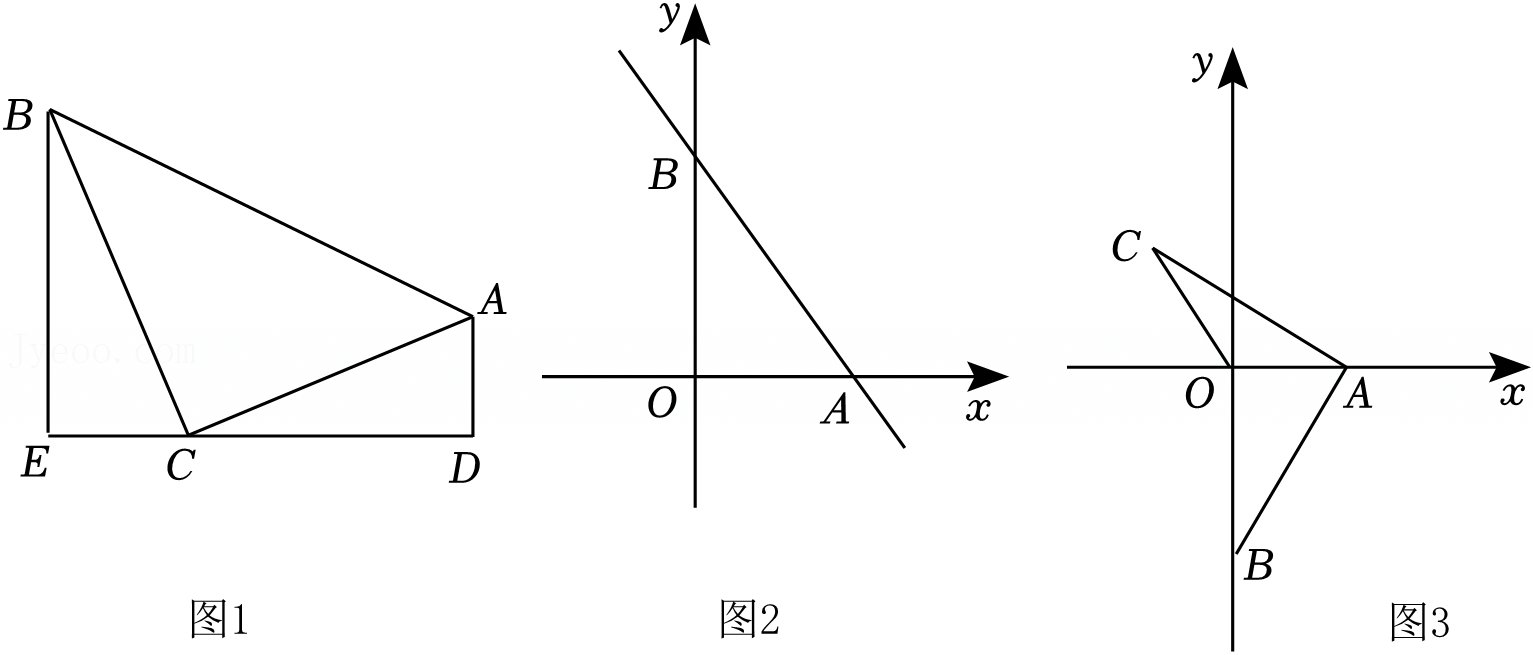
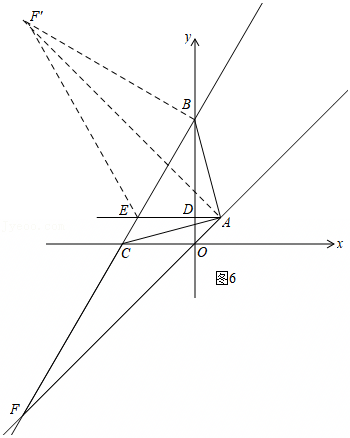
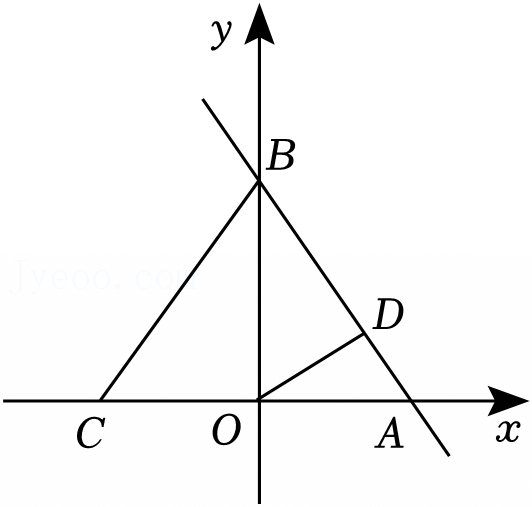
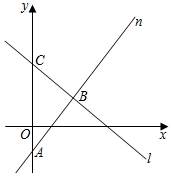 在如图的平面直角坐标系中,直线n过点A(0,-2),且与直线l交于点B(3,2),直线l与y轴交于点C.
在如图的平面直角坐标系中,直线n过点A(0,-2),且与直线l交于点B(3,2),直线l与y轴交于点C.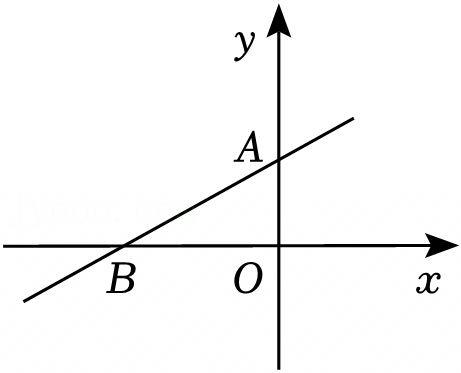
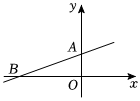
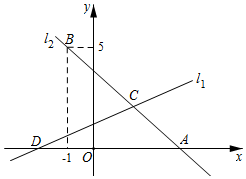 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m).
如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m).
qbb@dyw.com
2024-11-29
初中数学 | 八年级上 | 解答题