服务热线
搜题▪组卷
A.a2=5
B..{(﹣1)n+an}前2n项和为(2n+1)2
C..an=2n+1
D..![]()
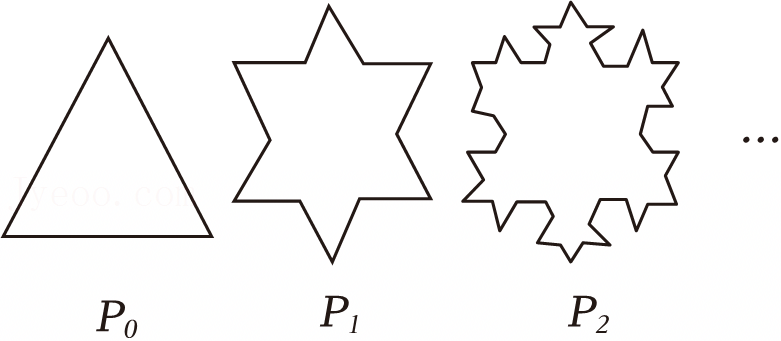
A.P3的边数为128
C.![]()
B.Pn的边数为3×4n
D..![]()
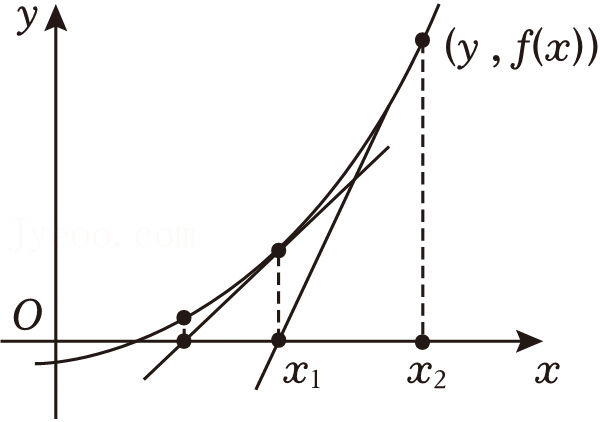
A.![]()
C..数列{an}是递减数列
B.数列{an}是等比数列
D..![]()

dygzsxyn
2025-03-15
高中数学 | | 多选题