AI助手
初中数学
21429.
（2020•铁一中学•八模）
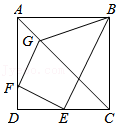
如图，正方形ABCD的边长为4，E、F分别为边CD、DA上的动点，点G在对角线AC上，且CG＝3AG，则四边形BEFG的周长的最小值为 ．
共享时间:2020-07-21
难度:4
[答案]
解：作G关于AD的对称点G′，作B点关于CD的对称点B′，连接G′B′，交BC于E，交AD于F，
此时BG+GF+EF+EB＝GB+B′G′，即此时四边形BEFG的周长最小，
∵正方形ABCD的边长为4，
∴AC＝4，
∵CG＝3AG，
∴AG＝，
∴TG＝AT＝1，
∴GS＝BH＝1，
∴G′H＝1+4＝5，HC＝4﹣1＝3，
∴B′H＝4+3＝7，
∴B′G′＝＝＝，
∵BG＝＝，
∴GB+B′G′＝+，
∴四边形BEFG的周长的最小值为+， 
纠错
收藏
下载
相似
组卷