服务热线
搜题▪组卷
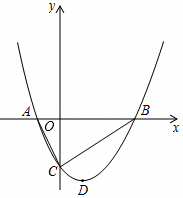
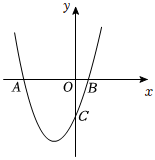 如图,在平面直角坐标系中,抛物线L1:y=ax2+4ax-6与x轴交于A和B(2,0)两点,并与y轴相交于点C.抛物线L2与L1关于坐标原点对称,点A、B在L2上的对应点分别为A′、B′.
如图,在平面直角坐标系中,抛物线L1:y=ax2+4ax-6与x轴交于A和B(2,0)两点,并与y轴相交于点C.抛物线L2与L1关于坐标原点对称,点A、B在L2上的对应点分别为A′、B′.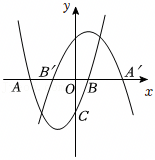

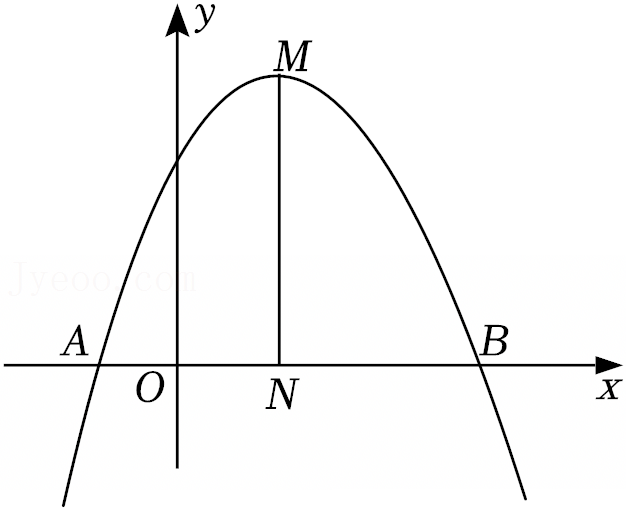
 如图,已知抛物线L:y=-x2+bx+c与x轴交于点B(-3,0)和点A(1,0),现将抛物线L沿y轴翻折,得到抛物线L1,点A和点B的对应点分别为A1和B1.
如图,已知抛物线L:y=-x2+bx+c与x轴交于点B(-3,0)和点A(1,0),现将抛物线L沿y轴翻折,得到抛物线L1,点A和点B的对应点分别为A1和B1.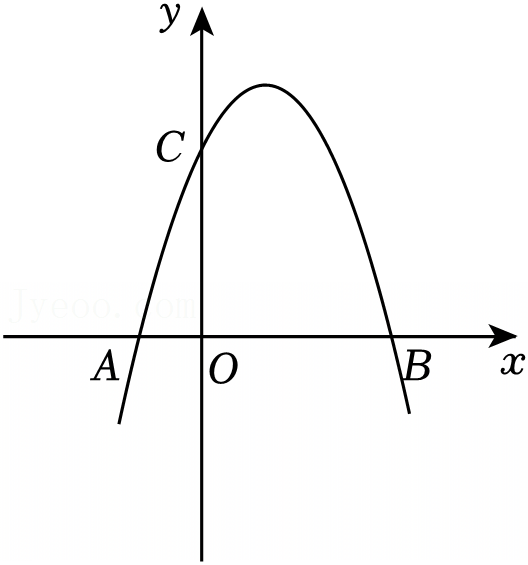



cl@dyw.com
2025-04-12
初中数学 | | 解答题