服务热线
搜题▪组卷
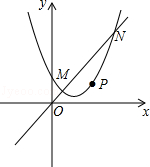
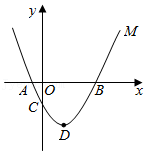
 已知二次函数y=ax2+bx+c(a>0)的图象与y轴相交于点A,y与x的部分对应值如表(m为整数):
已知二次函数y=ax2+bx+c(a>0)的图象与y轴相交于点A,y与x的部分对应值如表(m为整数):| x | 0 | m | 2 |
| y | -3 | -4 | -3 |
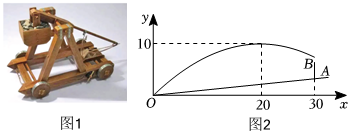

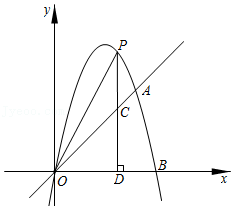
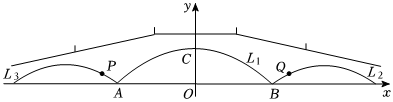
 从以动画技术革新领跑电影票房的《哪吒2》,到“神农”“天问”等楚才系列人形机器人集中亮相,现象级的科技飞跃成为今年春节的热门符号.某科技公司乘“巳”而上,在科技创新的驱动下,测试一款新研发的植护无人机喷洒农药,如图①,其喷洒轨迹可近似地看作抛物线型.如图②,已知无人机喷头A到水平地面(BC)的高度为3m,喷洒的农药覆盖农作物的宽度(BC)为4m,以线段BC所在直线为x轴,垂直于BC,且过线段BC的中点O与喷头A的直线为y轴,建立平面直角坐标系.
从以动画技术革新领跑电影票房的《哪吒2》,到“神农”“天问”等楚才系列人形机器人集中亮相,现象级的科技飞跃成为今年春节的热门符号.某科技公司乘“巳”而上,在科技创新的驱动下,测试一款新研发的植护无人机喷洒农药,如图①,其喷洒轨迹可近似地看作抛物线型.如图②,已知无人机喷头A到水平地面(BC)的高度为3m,喷洒的农药覆盖农作物的宽度(BC)为4m,以线段BC所在直线为x轴,垂直于BC,且过线段BC的中点O与喷头A的直线为y轴,建立平面直角坐标系.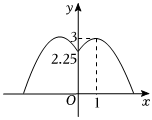 某小区有一个喷水池,中心处带有可升降喷头的喷水管垂直于地面,喷出的水流形状近似抛物线.如图是喷水池喷水时的截面图,以喷水池中心点O为原点,水平方向为x轴,喷水管竖直方向为y轴,建立平面直角坐标系.经测量,喷头位置在水池中心点O的正上方2.25m处,当水流满足距喷水管的水平距离为1m时,达到最大高度为3m.
某小区有一个喷水池,中心处带有可升降喷头的喷水管垂直于地面,喷出的水流形状近似抛物线.如图是喷水池喷水时的截面图,以喷水池中心点O为原点,水平方向为x轴,喷水管竖直方向为y轴,建立平面直角坐标系.经测量,喷头位置在水池中心点O的正上方2.25m处,当水流满足距喷水管的水平距离为1m时,达到最大高度为3m.
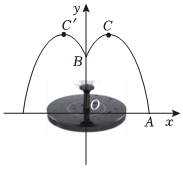 某乡间民宿的院子里安装了一个喷泉装置,喷泉底座安装在点O处,喷泉的出水口为点B,且OB=2m.如图,这是喷泉喷水时的截面示意图,根据实际情况调整喷泉落地点A,使点A到底座O的距离为4m.以过点O并垂直于地面的直线为y轴,OA所在直线为x轴,建立平面直角坐标系xOy,喷泉在y轴两侧的水流最高点C与C'之间的距离为3m,喷泉水流近似抛物线.
某乡间民宿的院子里安装了一个喷泉装置,喷泉底座安装在点O处,喷泉的出水口为点B,且OB=2m.如图,这是喷泉喷水时的截面示意图,根据实际情况调整喷泉落地点A,使点A到底座O的距离为4m.以过点O并垂直于地面的直线为y轴,OA所在直线为x轴,建立平面直角坐标系xOy,喷泉在y轴两侧的水流最高点C与C'之间的距离为3m,喷泉水流近似抛物线.
竹黎
2021-06-25
初中数学 | | 解答题