服务热线
搜题▪组卷
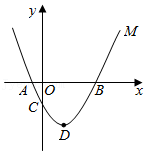
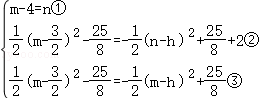
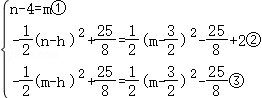
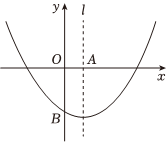
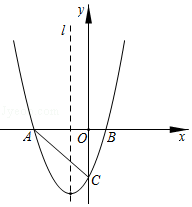
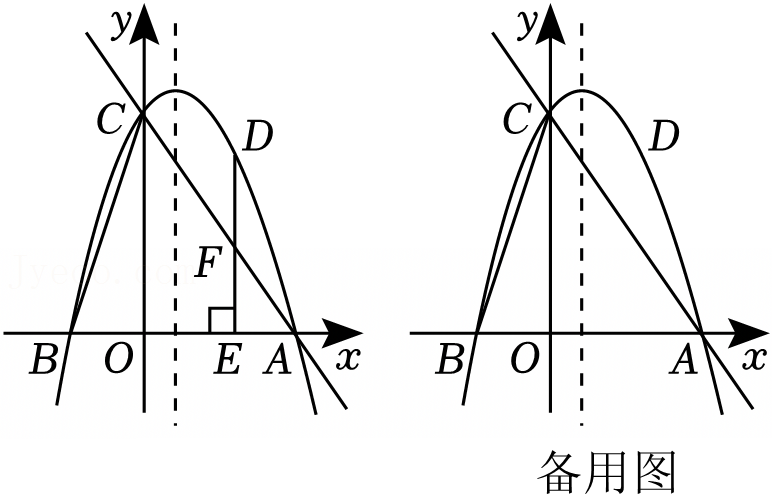
 如图,抛物线y=ax2+2x+c(a,c为常数,且a≠0)与x轴交于A、B两点,且与y轴交于点C(0,3),直线y=-x-1经过点A且与抛物线交于另一点D.
如图,抛物线y=ax2+2x+c(a,c为常数,且a≠0)与x轴交于A、B两点,且与y轴交于点C(0,3),直线y=-x-1经过点A且与抛物线交于另一点D.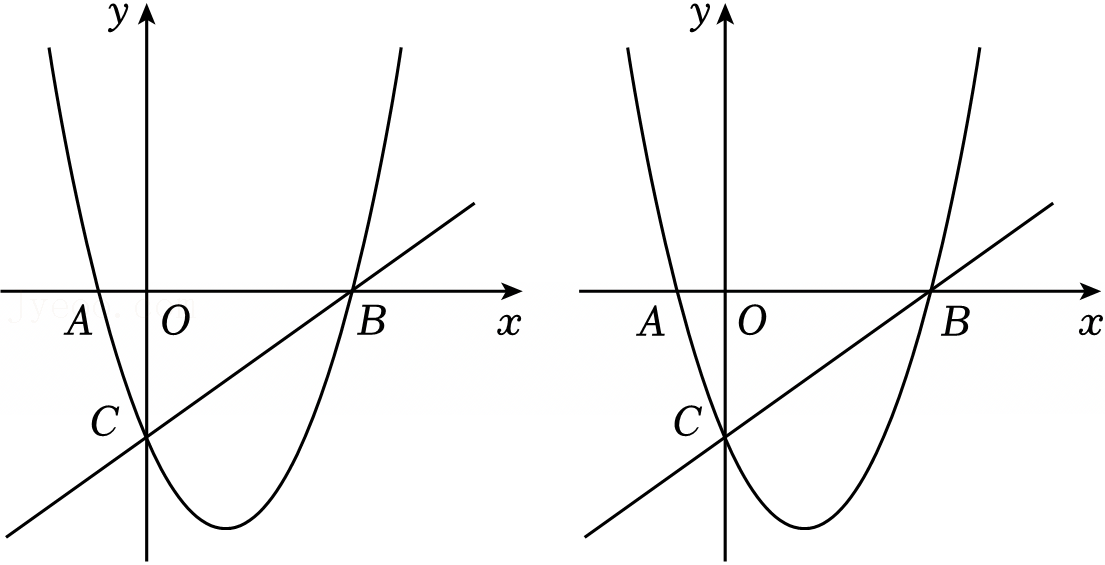
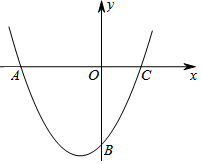
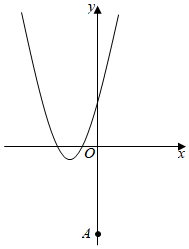 如图,抛物线W:y=x2+bx+c经过点(-3,0)和点(1,8).
如图,抛物线W:y=x2+bx+c经过点(-3,0)和点(1,8).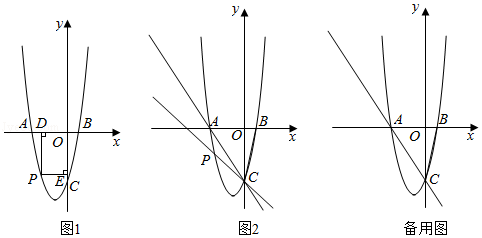

dysx2021
2021-07-25
初中数学 | | 解答题