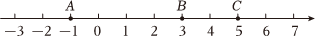在数轴上如果点表示的数记为点表示的数记为则两点间的距离可记作或如图所示数轴上三点表示的数分别为点为数轴上任意一点其表示的数为若则若点为线段上的任意一点求的值的最小值为此时的取值范围为

首页 > 试题列表 > 单题解析

197326. （2024•师大附中•七上期中）在数轴上，如果点A表示的数记为a,点B表示的数记为b,则A，B两点间的距离AB可记作|a-b|或|b-a|．如图所示，数轴上A，B，C三点表示的数分别为-1，3，5，点P为数轴上任意一点，其表示的数为x.
$德优题库$
（1）若AP=2，则x= ．
（2）若点P为线段上AC的任意一点，求|x-3|+|x+6|的值；
（3）PA+2PB+3PC的最小值为，此时x的取值范围为．

共享时间:2024-11-25 难度:4

纠错

下载

相似

组卷白板

[考点]

数轴，绝对值，有理数的混合运算，两点间的距离，

[答案]

（1）1或﹣3；

（2）当x＜﹣6时，|x﹣3|+|x+6|＝3﹣x﹣6﹣x＝﹣2x﹣3；

当﹣6≤x≤3时，|x﹣3|+|x+6|＝3﹣x+x+6＝9；

当x＞3时，|x﹣3|+|x+6|＝x﹣3+x+6＝2x+3；

（3）10；3≤x≤5．

[解析]

解：（1）数轴上A表示的数分别为﹣1，P表示的数为x，
则AP＝|x﹣（﹣1）|＝|x+1|＝2，
解得：x＝1或﹣3，
故答案为：1或﹣3；
（2）由|x﹣3|+|x+6|，
分三种情况：
当x＜﹣6时，|x﹣3|+|x+6|＝3﹣x﹣6﹣x＝﹣2x﹣3；
当﹣6≤x≤3时，|x﹣3|+|x+6|＝3﹣x+x+6＝9；
当x＞3时，|x﹣3|+|x+6|＝x﹣3+x+6＝2x+3；
（3）由于A，B，C三点表示的数分别为﹣1，3，5，点P表示的数为x，
则AP＝|x+1|，PB＝|x﹣3|，PC＝|x﹣5|，
∴PA+2PB+3PC＝|x+1|+2|x﹣3|+3|x﹣5|，
当x＜﹣1时，|x+1|+2|x﹣3|+3|x﹣5|＝﹣x﹣1﹣2x+6+15﹣3x＝﹣6x+20＞26；
当﹣1≤x≤3时，|x+1|+2|x﹣3|+3|x﹣5|＝x+1﹣2x+6+15﹣3x＝﹣4x+22，
此时10≤﹣4x+22≤26；
当3＜x≤5时，|x+1|+2|x﹣3|+3|x﹣5|＝x+1+2x﹣6+15﹣3x＝10；
当x＞5时，|x+1|+2|x﹣3|+3|x﹣5|＝x+1+2x﹣6+3x﹣15＝6x﹣20＞10；
综上所述：|x+1|+2|x﹣3|+3|x﹣5|的最小值为10，此时3≤x≤5，
故答案为：10；3≤x≤5．

[点评]

本题考查了"数轴，绝对值，有理数的混合运算，两点间的距离，"，属于"综合题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

172614. （2024•西安一中•七上一月）距离能够产生美．唐代著名文学家韩愈曾赋诗：“天街小雨润如酥，草色遥看近却无．”当代印度著名诗人泰戈尔在《世界上最遥远的距离》中写道：“世界上最遥远的距离不是瞬间便无处寻觅而是尚未相遇便注定无法相聚”距离，是数学、天文学、物理学中的热门话题．唯有对宇宙距离进行测量，人类才能掌握世界尺度．
$德优题库$
绝对值的定义：一个数在数轴上对应的点到原点的距离叫做这个数的绝对值．
例如：|3|是指数轴上表示3的点到原点的距离，|-6|是指数轴上表示-6的点到原点的距离．
【概念延伸】
①数轴上表示2和5的两点之间的距离是        ，|2-5|=        ；
②数轴上表示1和-3的两点之间的距离是        ，|1-（-3）|=        ．
【归纳总结】
点A，B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为|AB|，则|AB|=        ．
【拓展应用】
①数轴上表示数x和1的两点A和B之间的距离为|AB|=|x-1|，则|x-1|的最小值是        ，此时x的值为        ；
②数轴上表示数x和-1的两点A和B之间的距离为|AB|=        .如果|AB|=2，那么x的值为        ；
③式子|x+1|+|x-2|有最小值吗？若有，请求出它的最小值．

共享时间:2024-10-16 难度:4 相似度:1.5

解析

纠错

下载

组卷白板

27600. （2024•铁一中学•七上一月）结合数轴与绝对值的知识回答下列问题：
一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．
（1）例如：数轴上表示4和1的两点之间的距离为|4﹣1|＝　   　
数轴表示5和﹣2的两点之间的距离为|5﹣（﹣2）|＝|5+2|＝　   　
（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为　        　
数轴上表示数a的点与表示2的点之间的距离表示为　        　
若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；
（3）当a＝　   　时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为　   　．

共享时间:2024-10-21 难度:2 相似度:1.5

解析

纠错

下载

组卷白板

172839. （2024•逸翠园中学•七上一月）已知a，b互为相反数，且a≠0，c，d互为倒数，x的绝对值为1，求

的值．

共享时间:2024-10-10 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

172742. （2024•远东二中•七上一月）邮递员骑车从邮局出发，先向西骑行2km到达A村，继续向西骑行3km到达B村，然后向东骑行8km，到达C村，最后回到邮局．
（1）以邮局为原点，以向东方向为正方向，用1cm表示1km，画出数轴，并在该数轴上表示出A，B，C三个村庄的位置；
（2）C村距离A村有多远？
（3）邮递员共骑行了多少km？

共享时间:2024-10-16 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

172609. （2024•西安一中•七上一月）计算：
（1）24﹣（﹣16）+（﹣25）；
（2）

；
（3）（﹣3）×2×（﹣5）；
（4）

．

共享时间:2024-10-16 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

82685. （2024•铁一中学•七上期末）计算与化简求值：
（1）

；
（2）

；
（3）先化简再求值：

，其中x＝﹣4，y＝3．

共享时间:2024-02-13 难度:2 相似度:1.25

解析

纠错

下载

组卷白板

23562. （2020•铁一中学•七上期末）计算：
（1）﹣12×（

﹣

）+5；
（2）（﹣4）²×|﹣2|+9÷（﹣

）×

共享时间:2022-01-13 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

172629. （2024•长安区•月考）计算：

．

共享时间:2023-12-01 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

172461. （2024•师大附中•七上一月）计算．
（1）8+（﹣10）+（﹣2）﹣（﹣5）；
（2）

；
（3）

；
（4）2²×（﹣1）²×（﹣3）³．

共享时间:2024-10-22 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

172835. （2024•逸翠园中学•七上一月）计算：
（1）27﹣18+（﹣7）﹣32；
（2）

；
（3）

；
（4）

．

共享时间:2024-10-10 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

25655. （2024•漳州双语实验学校•七上期末）已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm,求CM的长．
$德优题库$

共享时间:2024-01-28 难度:2 相似度:1.25

解析

纠错

下载

组卷白板

23325. （2021•交大附中•七上期中）全运会期间出租车司机小王在南北走向的一段公路上运营，如果向北记作“+”，向南记作“-”．他这天的行车情况记录如下（单位：千米）-2，+5，-1，+10，-3，-2，-5，+6．
请回答：
（1）小王将最后一名乘客安全送到目的地时，在出发地的什么方向，距出发地多远？这天出租车行程总共是多少千米？
（2）若规定每趟车的起步价是10元，且每趟车3千米以内（含3千米）只收起步价；若超过3千米，除收起步价外，超过的每千米还需收1.2元钱．小王决定将这个时段的全部营业额捐给特殊学校，那么小王这个运营时段可以捐多少钱？