探究与实践问题发现用四个长为宽为的长方形拼成如图所示的正方形由此可以得到的等量关系是问题探究如图将边长为的正方形和边长为正方形拼在一起使得共线点落在上连接若的面积为求的长度问题解决如图某小区物业准备在小区内规划设计一块休闲娱乐区其中为两条互相垂直的道路且四边形与四边形为长方形

首页 > 试题列表 > 单题解析

196633. （2024•西工大附中•七上期末）探究与实践
问题发现：
（1）用四个长为a、宽为b的长方形拼成如图①所示的正方形ABCD，由此可以得到（a+b）²、（a-b）²、ab的等量关系是；
问题探究：
（2）如图②，将边长为a的正方形APCD和边长为b正方形BPEF拼在一起，使得A、P、B共线，点E落在PC上，连接AE，若AB=8，△APE的面积为7.5，求CE的长度；
问题解决：
（3）如图③，某小区物业准备在小区内规划设计一块休闲娱乐区，其中BE、CF为两条互相垂直的道路，且BG=CG，EG=FG，四边形ABGF与四边形CDEG为长方形，现计划在两个三角形区域种植花草，两个长方形区域铺设塑胶地面，按规划要求，道路BE的长度为80米，若种植花草每平方米需要100元，铺设塑胶地面每平方米需要30元，若物业为本次修建休闲娱乐区筹集了25万元，请你通过计算说明该物业筹集的资金是否够用？（道路的宽度均不计）
$德优题库$

共享时间:2024-02-19 难度:2

纠错

下载

相似

组卷白板

[考点]

完全平方公式的几何背景，整式的混合运算，

[答案]

（1）（a+b）²＝（a﹣b）²+4ab；

（2）2；

（3）该物业筹集的资金不够用，理由见解答．

[解析]

解：（1）根据题意得：（a+b）²＝（a﹣b）²+4ab；
故答案为：（a+b）²＝（a﹣b）²+4ab；
（2）设AP＝m，BP＝n，
∴AB＝AP+BP＝m+n＝8，
∵△APE面积为7.5，
∴

mn＝7.5，即mn＝15，
∵（m+m）²＝（m﹣n）²+4mn，
∴（m﹣n）²＝（m+n）²﹣4ab＝64﹣60＝4，
∴m﹣n＝2（负值舍去），
则CE＝PC﹣PE＝m﹣n＝2；
（3）该物业筹集的资金不够用，说明如下：
设BG＝CG＝s m，EG＝FG＝t m，
由题意得：BE＝BG+EG＝s+t＝80（m），
两个三角形区域的面积之和为

BG•CG+

FG•EG＝（

s²+

t²）（m²），
∴一共需要的资金为100（

s²+

t²）+30•2st＝（50s²+50t²+60st）元，
∵s+t＝80，
∴s²+t²＝（s+t）²﹣2st＝6400﹣2st，
∴50s²+50t²+60st＝50（6400﹣2st）+60st＝（320000﹣40st）元，
∵（s﹣t）²≥0，
∴（s+t）²﹣4st≥0，即st≤

＝1600，
∴40st≤64000，即320000﹣40st≥256000＞250000，
∴该物业筹集的资金不够用．

[点评]

本题考查了"完全平方公式的几何背景，整式的混合运算，"，属于"必考题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

25658. （2024•漳州双语实验学校•七上期末）探究与实践
问题发现：
（1）用四个长为a、宽为b的长方形拼成如图①所示的正方形ABCD，由此可以得到（a+b）²、（a-b）²、ab的等量关系是；
问题探究：
（2）如图②，将边长为a的正方形APCD和边长为b正方形BPEF拼在一起，使得A、P、B共线，点E落在PC上，连接AE，若AB=8，△APE的面积为7.5，求CE的长度；
问题解决：
（3）如图③，某小区物业准备在小区内规划设计一块休闲娱乐区，其中BE、CF为两条互相垂直的道路，且BG=CG，EG=FG，四边形ABGF与四边形CDEG为长方形，现计划在两个三角形区域种植花草，两个长方形区域铺设塑胶地面，按规划要求，道路BE的长度为80米，若种植花草每平方米需要100元，铺设塑胶地面每平方米需要30元，若物业为本次修建休闲娱乐区筹集了25万元，请你通过计算说明该物业筹集的资金是否够用？（道路的宽度均不计）
$德优题库$

共享时间:2024-01-28 难度:3 相似度:2

解析

纠错

下载

组卷白板

181313. （2024•未央区•七下二月）计算：

．

共享时间:2024-06-18 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

181463. （2024•铁一中学•七下二月）计算：
（1）

；
（2）x⁹÷x³﹣（2x³）²+2x•x⁵；
（3）2022²﹣2020×2024；
（4）（a+b﹣1）（a﹣b﹣1）．

共享时间:2024-06-19 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185103. （2025•铁一中学•七下期中）完全平方公式：（a±b）²＝a²±2ab+b²经过适当的变形，可以解决很多数学问题，请你解决下列问题：
（1）若x+y＝6，x²+y²＝28，则xy＝　　．
（2）若

，则

＝　　．
（3）已知（x﹣2023）（x﹣2025）＝5，求（x﹣2023）²+（x﹣2025）²的值．

共享时间:2025-05-15 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

180933. （2024•高新二中•七下一月）如图①是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图②）．
（1）根据上述过程，写出（a+b）²、（a-b）²、ab之间的等量关系：       ；
（2）利用（1）中的结论，若x+y=4，xy=1，则（x-y）²的值是        ；
（3）实际上通过计算图形的面积可以探求相应的等式，如图③，请你写出这个等式：       ；
（4）两个正方形ABCD，AEFG如图④摆放，边长分别为x,y,若x²+y²=34，BE=2，求图中阴影部分面积和．
$德优题库$

共享时间:2024-04-25 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

180263. （2024•逸翠园中学•七下二月）化简：
（1）x（x²y²-xy）-y（x²-x³y）÷x²y；
（2）（a+3）²-（a+1）（a-1）-2（2a+4）．

共享时间:2024-06-15 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

180125. （2024•长安区•七下二月） $德优题库$ 问题背景
如图，图1，图2分别是边长为（a+b），a的正方形，由图1易得（a+b）²=a²+2ab+b²．
类比探究
类比由图1易得公式（a+b）²=a²+2ab+b²的方法，依据图2中的已知条件推导出完全平方的另一个公式．
解决问题
（1）计算：（2m-n）²= ；
（2）运用完全平方公式计算：105²；
（3）已知（x+y）²=12，xy=2，求（x-y）²的值．

共享时间:2024-06-13 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

180123. （2024•长安区•七下二月）已知A=（2x+y）²-（x-2y）（4x+y），B=（2x²y+5xy²）÷xy-y（11x+3y）．
（1）求A和B；
（2）若x,y满足A+B=3，求4^x•32^y的值．

共享时间:2024-06-13 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185180. （2025•高新三中•七下期中）通过计算几何图形的面积可以验证一些代数恒等式．
$德优题库$
（1）如图①是一个大正方形被分割成了边长分别为a和b的两个正方形，长宽分别为a和b的两个长方形，利用这个图形可以验证公式，这种验证思路体现了下列哪一个数学思想．
A．数形结合
B．分类讨论
C．类比推理
D．转化
利用上述公式解决问题：
（2）根据上面得到的公式，若xy=2，x+y=5，则x²+y²= ．
（3）如图，在线段CE上取一点D，分别以CD、DE为边作正方形ABCD、DEFG，连接BG、CG、EG．若阴影部分的面积和为11，△CDG的面积为7，求CE的长度．

共享时间:2025-05-11 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

179971. （2024•航天中学•七下期中）计算：
（1）a²•a⁴-（a²）³；
（2）（3x-y-3）（3x-y+3）．

共享时间:2024-05-24 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

179875. （2024•爱知中学•七下期中）计算t
（1）（y²）³+y⁶．
（2）

（3）用乘法公式进行简便运算：199²．
（4）（2a+3）²﹣4（a+2）（a﹣2）．

共享时间:2024-05-28 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

179806. （2025•交大附中•八下期中）如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m＞n．（以上长度单位：cm）
（1）观察图形，发现代数式2m²+5mn+2n²可以因式分解为　　；
（2）若每块小矩形的面积为12cm²，四个正方形的面积和为50cm²，试求图中所有裁剪线（虚线部分）的长度之和．

共享时间:2025-05-24 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

179777. （2025•交大附中•七下期中）计算：
（1）（-2x）³•x²+x•x⁴；
（2）（x-5）（2x+5）+2x（3-x）．

共享时间:2025-05-12 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

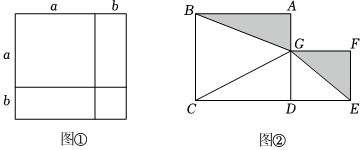
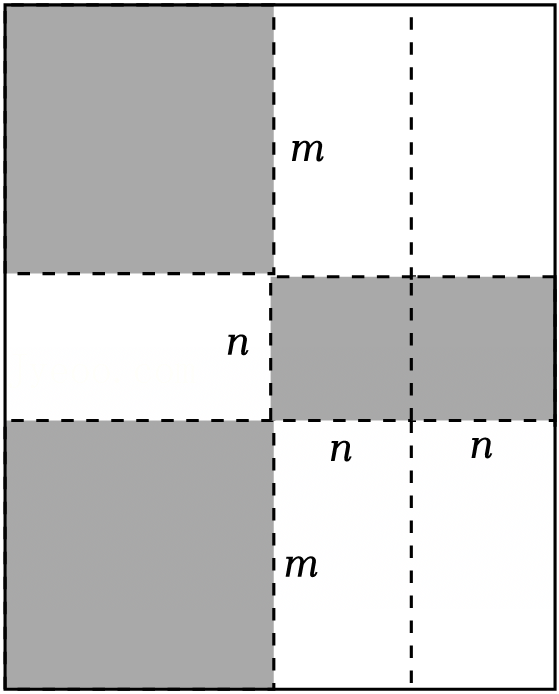
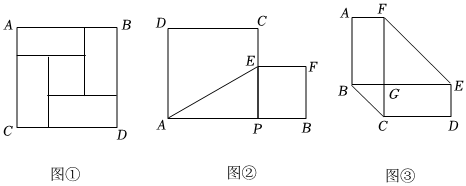
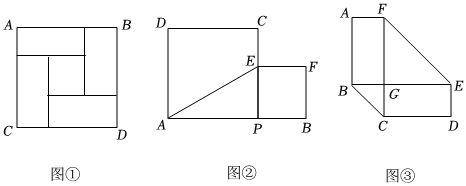
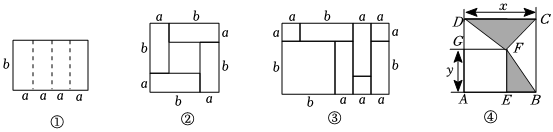
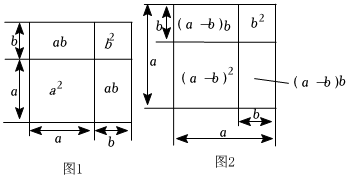
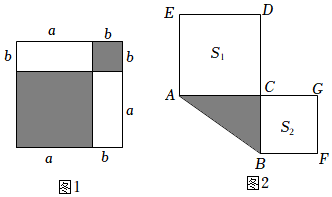185373. （2024•高新一中•七下期中） $德优题库$ 图形是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，而运用代数思想也能巧妙的解决一些图形问题．
（1）用两个长为a,宽为b的长方形，和两个边长分别为a和b的正方形，按图1的形状拼成一个大正方形．若a+b=5，ab=4，则a²+b²的值为；
（2）万物复苏的春天，美丽校园中浅浅的绿意渲染出浓浓的生气，学校计划在如图2的两块正方形草地间种些花，以淡淡的花香装点烈烈的校园书香，两块草地分别是以AC、BC为边的正方形，且面积和S₁+S₂=25，点C是线段AG上的点，若AG=7，求用来种花的部分的面积．

共享时间:2024-05-18 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185499. （2024•高新一中•七下期中） $德优题库$ “数缺形时少直观，形缺数时难入微．数形结合百般好，隔裂分家万事休．”数形结合是解决数学问题的重要思想方法．如图1，是一个长为2m,宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形．
（1）请用两种不同的方法表示出图2中阴影部分的面积．
方法1：；方法2：；
（2）由（1）可得三个代数式（m+n）²，（m-n）²，mn之间的等量关系是；
（3）若图1中每块小长方形的周长为16，面积为5，求图2阴影部分的面积．

共享时间:2024-05-16 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

ztp@dyw.com

2024-02-19

初中数学 | 七年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2023-2024学年陕西省西安市碑林区西北工大附中七年级（上）期末数学试卷

更新:2024-02-19 05:30浏览量:25

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手