服务热线
搜题▪组卷
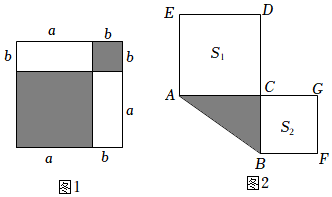
 我们知道,将完全平方公式(a±b)2=a2±2ab+b2适当的变形,可以解决很多数学问题,请你观察、思考,并解决以下问题:
我们知道,将完全平方公式(a±b)2=a2±2ab+b2适当的变形,可以解决很多数学问题,请你观察、思考,并解决以下问题: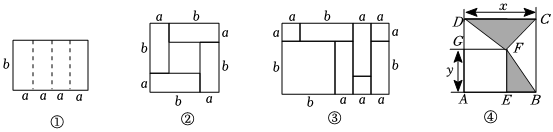
 小明在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.
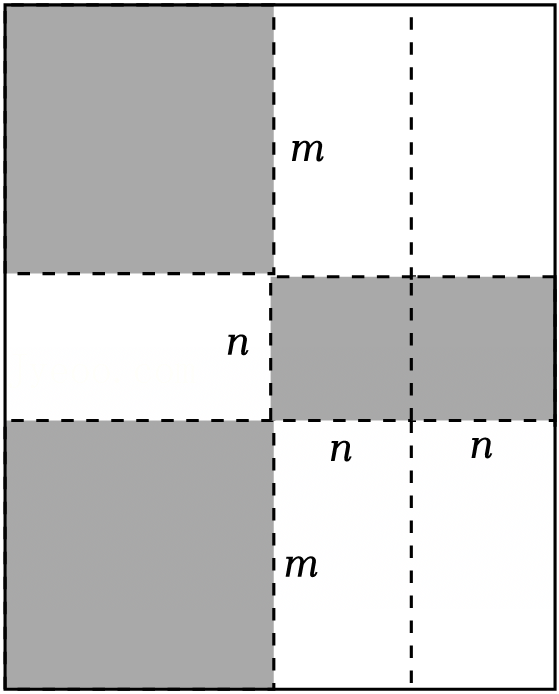
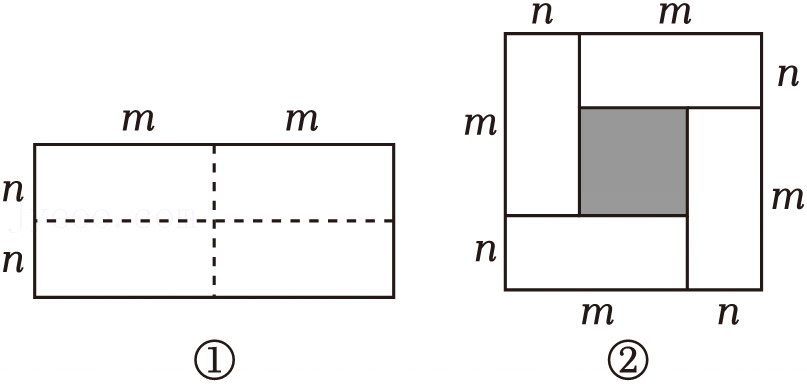
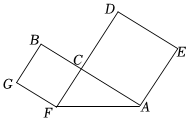
小明在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.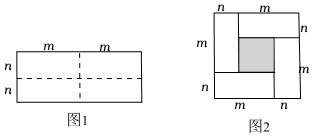 “数缺形时少直观,形缺数时难入微.数形结合百般好,隔裂分家万事休.”数形结合是解决数学问题的重要思想方法.如图1,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
“数缺形时少直观,形缺数时难入微.数形结合百般好,隔裂分家万事休.”数形结合是解决数学问题的重要思想方法.如图1,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.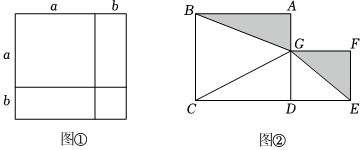
 图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.
图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.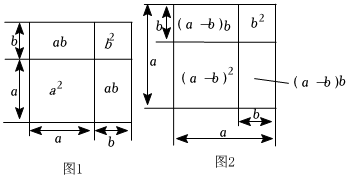 问题背景
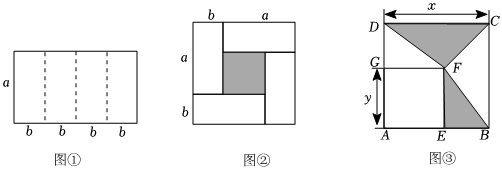
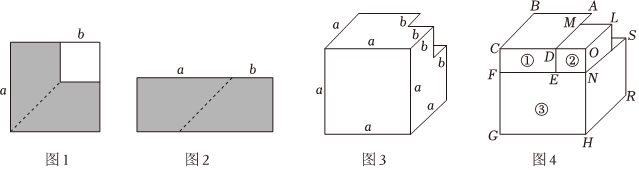
问题背景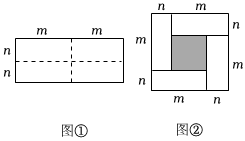 图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀将其平均分成四个小长方形,然后按图②所示拼成一个正方形.
图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀将其平均分成四个小长方形,然后按图②所示拼成一个正方形.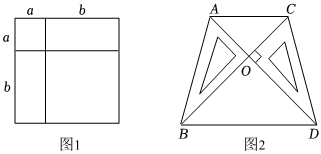
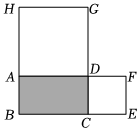
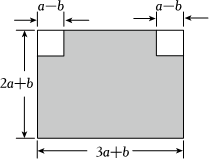 如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a-b)米的小正方形空地.
如图,和谐广场有一块长为(3a+b)米,宽为(2a+b)米的长方形土地,现要将阴影部分进行绿化,在上方两角处留两块边长为(a-b)米的小正方形空地.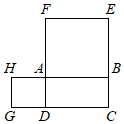
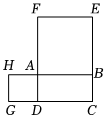 完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
lc@dyw.com
2025-05-24
初中数学 | 八年级下 | 解答题