服务热线
搜题▪组卷
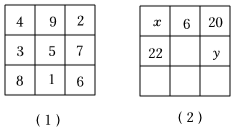幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方．图（2）是一个未完成的幻方，则x与y的和是（ ）
，
，
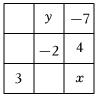“九宫图”传说是远古时代洛河中的一个神龟背上的图案，故又称“龟背图”，中国古代数学史上经常研究这一神话．数学上的“九宫图”所体现的是一个3×3表格，其每行、每列、每条对角线上三个数字之和都相等，也称为三阶幻方，如图是一个三阶幻方，则2x+y的值为（ ）
据记载，“幻方”源于我国古代的“洛书”，是世界上最早的矩阵．如图所示的幻方是由3×3的方格构成，每一行、每一列以及每一条对角线上的三个数字或字母的和均相等，则a的值为（ ）
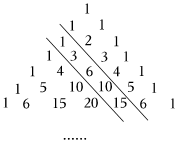如图，被称为“杨辉三角”或“贾宪三角”．其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和．表中两平行线之间的一列数：1，3，6，10，15，…，我们把第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为an，则a4+a200=（ ）
A.6x+4（8-x）=38
C.8x+6x=38
B.4x+6x=38
D.4x+6（8-x）=38
A.6x+4（8-x）=38
C.4x+6（8-x）=38
B.4x+6x=38
D.8x+6x=38
A.7x-9=9x-7
C.7x-7=9x-9
B.7（x+1）=9（x-1）
D.7（x-1）=9（x+1）
A.3x﹣2＝2x+9
C.3（x﹣2）＝2x+9
B.
+2＝
﹣9
D.
＝
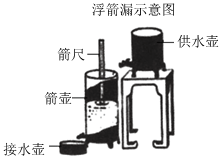《九章算术》中记载，浮箭漏（如图）可通过读取箭尺读数计算时间．某学校实验小组仿制了一套浮箭漏，每2小时记录一次箭尺读数，得到如表数据：| 供水时间x（小时） | 0 | 2 | 4 | 6 | 8 |
| 箭尺读数y（厘米） | 6 | 18 | 30 | 42 | 54 |
A.当x=4时，y=30
C.随着x的增加，y逐渐增加
B.当x=7时，y=48
D.x每增加1小时，y增加12厘米
A.
C.
B.
D.．
fd@dyw.com
2024-12-11
初中数学 | 八年级上 | 选择题
纠错
收藏
下载
相似
组卷
解析
在长方形ABCD中，放入5个形状大小相同的小长方形（空白部分），其中AB=7cm,BC=11cm,则阴影部分图形的总面积为（ ）cm2
