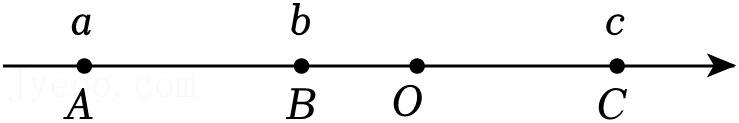首页 | 客服 | 上传赚现
计算题
1道
设置组卷 进入组卷
初中数学
同步组卷 细目组卷 错题组卷 试卷组卷 中考组卷 试卷中心 共享课件 共享练考 共享学校
(1)
设置组卷 进入组卷

服务热线

400-816-0029

    自建题库，共享分红

德优题库QQ交流群

首页 > 试题列表 > 单题解析
173158. （2024•高新二中•七上一月） 阅读理解：数轴是一个非常重要的数学工具，使数和数轴上的点建立起对应关系，这样能够用“数形结合”的方法解决一些问题．数轴上，若A，B两点分别表示数a、b,那么A，B两点之间的距离与a,b两数的差有如下关系：AB=|a-b|或|b-a|、如|5-3|表示5、3在数轴上对应的两点之间的距离．
问题（1）：当x的值取在        的范围时，|x-1|+|x+3|的最小值是        ；
问题（2）：当x=        时，|x+1|+|x-2|+|x-4|的最小值是        ；
问题（3）：若|x+1|+|x-a|的最小值是5，求a的值．
问题（4）：已知（|x+1|+|x-2|）×（|y-2|+|y+1|）×（|z-3|+|z+1|）=36，则求出x+y+z的最大值和最小值．
共享时间:2024-10-10 难度:3
纠错 收藏 下载 相似 组卷
[考点]
数轴，绝对值，有理数的减法，
[答案]
问题（1）：﹣3≤x≤1；4；问题（2）：2；5；问题（3）：4或﹣6；问题（4）：最大值为7，最小值为﹣3．
[解析]
解：问题（1）：|x﹣1|+|x+3|表示数x在数轴上对应的点到数1和﹣3表示的点的距离之和，则当x在数1和﹣3之间时，数x在数轴上对应的点到数1和﹣3的距离之和最小，
即当﹣3≤x≤1时，|x﹣1|+|x+3|的最小值是1﹣（﹣3）＝4；
故答案为：﹣3≤x≤1；4；
问题（2）：原式表示数x在数轴上对应的点到数﹣1，2，4表示的点的距离之和，则当x与数2重合时，表示数x在数轴上对应的点到数﹣1，2，4表示的点的距离之和最小，
即当x＝2时，|x+1|+|x﹣2|+|x﹣4|的最小值是4﹣（﹣1）＝5；
故答案为：2；5；
问题（3）：原式表示数x在数轴上对应的点到数﹣1和a表示的点的距离之和，则当x在数﹣1和a之间时，数x在数轴上对应的点到数﹣1和a的距离之和最小，最小值为|a+1|，
∵|x+1|+|x﹣a|的最小值是：5，
∴|a+1|＝5，
解得：a＝4或﹣6；
问题（4）：|x+1|+|x﹣2|的最小值为：3，
|y﹣2|+|y+1|的最小值为3，
|z﹣3|+|z+1|的最小值为4，
∴（|x+1|+|x﹣2|）×（|y﹣2|+|y+1|）×（|z﹣3|+|z+1|）≥36，
∵（|x+1|+|x﹣2|）×（|y﹣2|+|y+1|）×（|z﹣3|+|z+1|）＝36，
∴|x+1|+|x﹣2|＝3，|y﹣2|+|y+1|＝3，|z﹣3|+|z+1|＝4，
∴﹣1≤x≤2，﹣1≤y≤2，﹣1≤z≤3，
∴﹣3≤x+y+z≤7，
即最大值为7，最小值为﹣3．
[点评]
本题考查了"数轴，绝对值，有理数的减法，"，属于"典型题"，熟悉题型是解题的关键。
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！ ！版权申诉
174096. （2024•铁一中学•七上一月） 已知|x|=2，|y|=4，且x＞y,求x-y的值．
共享时间:2024-10-12 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
192069. （2023•高新一中•七上二月） 德优题库已知有理数a＞0，b＜0，c＞0，且|c|＜|b|＜|a|．
（1）在如图所示的数轴上将a,b,c三个数表示出来；
（2）化简：2|a-c|+|b+c|-|a-b|．
共享时间:2023-12-18 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
173108. （2024•高新三中•七上一月） 德优题库有理数a,b,c在数轴上的位置如图所示．
（1）用“＞”“＜”或“=”填空：
a+b        0，c-a        0，b+2        0．
（2）化简：|a+b|+2|c-a|-|b+2|．
共享时间:2024-10-22 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
175882. （2024•交大附中•七上一月） ．由绝对值的几何意义可知，数轴上表示数a的点到原点的距离为|a|．小小进一步探究发现，在数轴上，表示3和5的两点之间的距离为|5﹣3|＝2；表示﹣3和5的两点之间的距离为|﹣3﹣5|＝8；表示﹣3和﹣5的两点之间的距离为|﹣3﹣（﹣5）|＝2．
根据以上内容回答下列问题：
（1）数轴上表示﹣1和5的两点之间的距离为 　  ．
（2）若|x﹣5|＝2，则x＝　   　；
（3）若|x+2|+|x﹣4|＝8，则x＝　    　．
共享时间:2024-10-12 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
185324. （2023•高新三中•七上一月） 阅读下面材料：点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|，当A、B两点都不在原点时，
德优题库
点A、B都在原点的右边，如图2，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
点A、B在原点的左边，如图3，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
点A、B在原点的两边，如图4，|AB|=|OA|+|OB|=|a|+|b|=a+（-b）=|a-b|．
综上，数轴上A、B两点的距离|AB|=|a-b|．
回答下列问题：
（1）数轴上表示2和5的两点之间的距离是        ，数轴上表示-2和-5的两点之间的距离是        ，数轴上表示1和-3的两点之间的距离是        ；
（2）数轴上表示x和-1的两点A和B之间的距离是        ，如果|AB|=2那么x为        ．
（3）当代数式|x+1|+|x-2|取最小值时，相应x的取值范围是        ．
共享时间:2023-10-13 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
27600. （2024•铁一中学•七上一月） 结合数轴与绝对值的知识回答下列问题：
一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．
（1）例如：数轴上表示4和1的两点之间的距离为|4﹣1|＝　   　
数轴表示5和﹣2的两点之间的距离为|5﹣（﹣2）|＝|5+2|＝　   　
（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为　        　
数轴上表示数a的点与表示2的点之间的距离表示为　        　
若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；
（3）当a＝　   　时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为　   　．
共享时间:1970-01-01 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
175471. （2024•理工大附中•七上二月） 已知|a|=5，|b|=3，且|a-b|=b-a,求a-b的值．
共享时间:2024-12-22 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
173577. （2024•铁一中学•九上一月） 德优题库结合数轴与绝对值的知识回答下列问题：
一般地，数轴上表示数m和数n的两点之间的距离公式为|m-n|．
（1）例如：数轴上表示4和1的两点之间的距离为|4-1|=       
数轴表示5和-2的两点之间的距离为|5-（-2）|=|5+2|=       
（2）数轴上表示数a的点与表示-4的点之间的距离表示为       
数轴上表示数a的点与表示2的点之间的距离表示为       
若数轴上a位于-4与2之间，求|a+4|+|a-2|的值；
（3）当a=       时，|a+5|+|a-1|+|a-4|的值最小，最小值为       ．
共享时间:2024-10-13 难度:2 相似度:1.67
解析 纠错 收藏 下载 组卷
174788. （2024•灞桥区•七上一月） 德优题库【知识引导】在数轴上，两点之间的距离可以用这两点在数轴上所对应数的差的绝对值来表示，例：点M表示的数为2，点N表示的数为-1，则点M，N之间的距离为|2-（-1）|=3．
【实际应用】如图，在一条数轴上，从左往右的点A，B，C表示的数分别是-3，b,6．
（1）点A到原点的距离是        ，A，C两点之间的距离是        ；
（2）已知点B和点C之间的距离是2，一动点P从点B出发，以每秒1个单位长度的速度沿数轴向左匀速运动，5秒后，点P表示的数是多少？
（3）已知点D在点A的左侧，和点A的距离是2个单位长度，一动点Q从点D出发，沿数轴运动，下表是小俊记录的点Q运动的情况（沿数轴向右运动记为正，向左运动记为负，例如“-2”表示向左运动2个单位长度，“+4”表示向右运动4个单位长度），在第几次运动后点Q与点D的距离最远，此时点Q表示的数是多少？
第1次 第2次 第3次 第4次
-2 +4 -8 -1
共享时间:2024-10-19 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
174716. （2024•滨河中学•七上一月） 德优题库【知识准备】数轴上A、B两点对应的数分别为a、b,则A、B两点之间的距离表示为：AB=|a-b|．
【问题探究】
（1）如图，点A在数轴上表示的数是8，点B在数轴上表示的数是-10，则AB=       ；
（2）在（1）的条件下，动点P从点A出发，以每秒2个单位长度的速度沿数轴匀速向右运动；同时动点Q从点B出发，以每秒4个单位长度的速度沿数轴匀速向右运动，设P，Q两点的运动时间为t秒，当PQ=8时，求t的值；
（3）在（1）的条件下，动点M从点A出发，以每秒2个单位长度的速度向点B匀速运动；同时点N从点B出发，以每秒3个单位长度的速度向点A运动．当点M到达点B后，立即以原速返回，到达点A停止运动，当点N到达点A后，立即以原速返回，到达点B停止运动，请问：当点M运动时间为        秒时，MN=7．（直接写出答案，不写解题过程）
共享时间:2024-10-23 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
173576. （2024•铁一中学•九上一月） 已知有理数a,b满足|a|=2，|b|=3，且|a+b|=a+b,求a-b的值．
共享时间:2024-10-13 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
174714. （2024•滨河中学•七上一月） 德优题库有理数a,b在数轴上的位置如图，
（1）a        0，b        0，|a|       |b|（用“＜”“＞”“=”填空）；
（2）化简：|a|-|b|+|-a+b|．
共享时间:2024-10-23 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
172843. （2024•逸翠园中学•七上一月） 已知有理数a，b，c在数轴上的对应点分别是A，B，C，其位置如图所示．
（1）若|a+5|+（c﹣3）2＝0，B为数轴上一动点，B表示的数为b，则|b﹣a|+|b﹣c|最小值为 　8　；
（2）化简|b+c|﹣|a﹣c|﹣|a+b|．

共享时间:2024-10-10 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
173952. （2024•西工大附中•七上一月） 在数轴上表示下列各数，并用“＜”连接起来．
|﹣4|，﹣2.5，﹣1，0，．
共享时间:2024-10-13 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷
179527. （2024•爱知中学•七上期中） 画出数轴，在数轴上表示下列各数，并用“＜”将它们连接起来．
2，0，﹣1.5，|﹣3|，．
共享时间:2024-11-22 难度:3 相似度:1.34
解析 纠错 收藏 下载 组卷

dyczsxyn

2024-10-10

初中数学 | 七年级上 | 解答题

  • 下载量
  • 浏览量
  • 收益额
  • 0
  • 5
  • 0
相同试题
试题下载
试题内容
调用试题名称
共享人
唐老师
试题题型
解答题
试题难度
试题题源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试题下载至自主题库后，下载、备课永久免费！
试卷设置
试卷名称
省市校区
阶段科目
年份卷型
选择类型
已选考点
在线训练
是 否
视频讲解
温馨提示
视频讲解正在加载中、请等待！
视频解析购买
支付方式
德优币数
本次消耗0德优币
温馨提示

客服电话：400-816-0029，服务邮箱：610066832@qq.com

视频资源

试题找茬
纠错类型
纠错描述
温馨提示
共享试题、试卷经平台审核通过后方可展示，并永久享用用户下载分红权！