我们知道在数轴上表示数到原点的距离这是绝对值的几何意义进一步地数轴上两个点分别用表示那么两点之间的距离为利用此结论回答以下问题数轴上表示和的两点之间的距离是如果那么是式子的最小值是的最小值是灵活应用某市环形线路上顺次有个站点分别记为各站

首页 > 试题列表 > 单题解析

173107. （2024•高新三中•七上一月）我们知道，在数轴上，|a|表示数a到原点的距离，这是绝对值的几何意义．进一步地，数轴上两个点A、B，分别用a、b表示，那么A、B两点之间的距离为：AB=|a-b|．利用此结论，回答以下问题：
（1）数轴上表示x和-1的两点A，B之间的距离是       ，如果|AB|=2，那么x是       ；
（2）式子|x+1|+|x-2|+|x-3|的最小值是       ；
（3）|x+1|+2|x-2|+3|x-3|的最小值是       ；
（4）灵活应用：某市环形线路上顺次有4个站点，分别记为A、B、C、D，各站点分别配备了物资9份、12份、7份、16份，AB、BC、CD、DA之间的路程分别为4km,4km,3km,2km,且每份物资每千米运费为100元，现为使各站点的物资数相等，各向相邻站点移交装备若干份，且要使移交的运费最少，则各站点分别向相邻的站点移交了多少份物资？移动的总运费是多少？

共享时间:2024-10-22 难度:4

纠错

下载

相似

组卷白板

[考点]

数轴，绝对值，一元一次方程的应用，两点间的距离公式，

[答案]

（1）|x+1|；1或﹣3；

（2）4；

（3）6；

（4）由B→^1份C，D→^3份C，D→^2份A，移交的运费最少，移动的总运费是1700元．

[解析]

解：（1）数轴上表示x和﹣1的两点A，B之间的距离是|x﹣（﹣1）|＝|x+1|，
如果|AB|＝2，则|x+1|＝2那么x是1或﹣3；
故答案为：|x+1|；1或﹣3；
（2）|x+1|+|x﹣2|+|x﹣3|表示：数轴上的点x到﹣1，2和3距离的和，
当x在数2所对应的点时值最小，有最小值是4．
故答案为：4；
（3）当x≤﹣1时，原式＝﹣x﹣1﹣2x+4﹣3x+9＝﹣6x+12≥18；
当﹣1＜x≤2时，原式＝x+1﹣2x+4﹣3x+9＝﹣4x+14，
∴6≤﹣4x+14＜18；
当2＜x≤3时，原式＝x+1+2x﹣4﹣3x+9＝6；
当x＞3时，原式＝x+1+2x﹣4+3x﹣9＝6x﹣12＞6，
∴|x+1|+2|x﹣2|+3|x﹣3|的最小值是6；
故答案为：6；
（4）（9+12+7+16）÷4＝11（份），
方法一：B→^1份C，运费为1×4×100＝400（元）；
D→^3份C，运费为3×3×100＝900（元）；
D→^2份A，运费为2×2×100＝400（元）；
方法一的总运费为400+900+400＝1700（元）；
方法二：B→^1份A，运费为1×4×100＝400（元）；
D→^1份A，运费为1×2×100＝200（元）；
D→^4份C，运费为4×3×100＝1200（元）；
方法二的总运费为400+200+1200＝1800（元）；
1700＜1800，
∴由B→^1份C，D→^3份C，D→^2份A，移交的运费最少，移动的总运费是1700元．

[点评]

本题考查了"数轴，绝对值，一元一次方程的应用，两点间的距离公式，"，属于"综合题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

27692. （2024•高新一中•七上一月）已知C，D两点将线段AB分为三部分，且AC：CD：DB=2：3：4，若AB的中点为M，BD的中点为N，且MN=5cm,求AB的长．

共享时间:2023-12-16 难度:2 相似度:1.5

解析

纠错

下载

组卷白板

27600. （2024•铁一中学•七上一月）结合数轴与绝对值的知识回答下列问题：
一般地，数轴上表示数m和数n的两点之间的距离公式为|m﹣n|．
（1）例如：数轴上表示4和1的两点之间的距离为|4﹣1|＝　   　
数轴表示5和﹣2的两点之间的距离为|5﹣（﹣2）|＝|5+2|＝　   　
（2）数轴上表示数a的点与表示﹣4的点之间的距离表示为　        　
数轴上表示数a的点与表示2的点之间的距离表示为　        　
若数轴上a位于﹣4与2之间，求|a+4|+|a﹣2|的值；
（3）当a＝　   　时，|a+5|+|a﹣1|+|a﹣4|的值最小，最小值为　   　．

共享时间:2024-10-21 难度:2 相似度:1.5

解析

纠错

下载

组卷白板

23569. （2020•铁一中学•七上期末）如图，数轴上线段AB=2（单位长度），CD=4（单位长度），点A在数轴上表示的数是-10，点C在数轴上表示的数是16．若线段AB以6个单位长度/秒的速度向右匀速运动，同时线段CD以2个单位长度/秒的速度向左匀速运动．设运动的时间为t秒，请解决下列问题：
（1）当t=1时，A点表示的数为，此时BC= ；
（2）当运动到BC=6（单位长度）时，求运动时间t的值；
（3）P是线段AB上一点，当点B运动到线段CD上时，若关系式BD-AP=4PC成立，请直接写出此时线段PD的长：PD= ．
$德优题库$

共享时间:2021-04-12 难度:5 相似度:1.5

解析

纠错

下载

组卷白板

23324. （2021•交大附中•七上期中）根据图中给出的数轴解答问题：
$德优题库$
（1）请你根据图中A，B两点的位置（点B到表示-2和-3两点的距离相等），分别写出A，B所表示的有理数        ，       ；
（2）观察数轴，与点A的距离为4的点表示的数是        ；
（3）如果将数轴折叠，使得点A与表示-2的点重合，则点B与表示数        的点重合；
（4）如果数轴上M、N两点之间的距离为2021（点M在点N的左侧，且MN两点经过（3）中的折叠后互相重合，则M、N两点所表示的数分别是多少？

共享时间:2021-12-25 难度:4 相似度:1.5

解析

纠错

下载

组卷白板

23041. （2021•铁一中学•七上期中）【知识准备】：数轴上A、B两点对应的数分别为a、b，则A、B两点之间的距离表示为：AB＝|a﹣b|．
【问题探究】：数轴上A、B两点对应的数分别为a、b，且满足|a+2|+（b﹣6）²＝0．
（1）求得A、B两点之间的距离是　　；
（2）若在数轴上有一点M，满足BM＝4AM，求点M表示的数；
（3）若P、Q两点在数轴上运动，点P从A出发以2个单位长度/秒的速度向右匀速运动，同时，点Q从B出发以3个单位长度/秒的速度向左匀速运动．经过　　秒，P、Q相距2个单位长度；
（4）原点O在数轴上表示0，点N在数轴上表示3，若A、O两点在数轴上以2个单位长度/秒的速度同时向右匀速运动，与此同时，B、N以3个单位长度/秒的速度在数轴上向左匀速运动，在这个过程中，有一段时间，A、O两点都运动在线段BN上，则这段时间的时长是　　秒．

共享时间:2021-11-22 难度:4 相似度:1.35

解析

纠错

下载

组卷白板

1. （2013•邢台市•模拟）某商店积压了100件某种商品，为让这些商品尽快脱手，该商店店主采取了如下销售方案：将标价提高到进价的2.5倍，再作三次降价处理，第一次打出“亏本价”，按标价的七折销售，第二次标出“破产价”，在第一次降价的基础上再降价30%，第三次标出“跳楼价”，是进价的0.98．结果第一次降价处理，仅售出10件；第二次降价处理，售出50件；第三次降价处理，剩下商品被一抢而空．经该店店主核算，这100件商品毛利润为3590元，则该商品的进价是多少元（毛利润＝卖价﹣进价）．

共享时间:2021-05-17 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

23568. （2020•铁一中学•七上期末）请列一元一次方程解应用题
肉夹馍和凉皮是西安特色美食，小华一放假就和同学迫不及待地相约一起去美食街吃凉皮肉夹馍．几个同学开始在店里吃了4碗凉皮4个肉夹馍，共花费72元；后又打包6碗凉皮10个肉夹馍，共花费148元．请问，一碗凉皮和一个肉夹馍的分别是多少元？

共享时间:2022-01-13 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

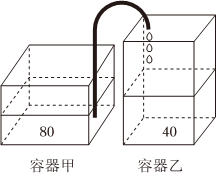61389. （2023•爱知中学•七上期末） $德优题库$ 如图，甲、乙两个长方体容器放置在同一水平桌面上，容器甲的底面积为80dm²，高为6dm；容器乙的底面积为40dm²，高为9dm.容器甲中盛满水，容器乙中没有水，现从容器甲向容器乙匀速注水，每分钟注水30dm³．
（1）容器甲中水位的高度每分钟下降 dm,容器乙中水位的高度每分钟上升 dm；
（2）从容器甲开始注水起，经过多长时间，两个容器中水位的高度相差3dm？

共享时间:2023-02-19 难度:2 相似度:1.25

解析

纠错

下载

组卷白板

61336. （2023•爱知中学•九上期末）某商品进价为200元，若按标价的七五折销售，则利润率为20%，求这件商品的标价．

共享时间:2023-03-02 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

25679. （2023•陕西省•真题）小红在一家文具店买了一种大笔记本4个和一种小笔记本6个，共用了62元．已知她买的这种大笔记本的单价比这种小笔记本的单价多3元，求该文具店中这种大笔记本的单价．

共享时间:2023-07-20 难度:2 相似度:1.25

解析

纠错

下载

组卷白板

25654. （2024•漳州双语实验学校•七上期末）列方程解决下面问题：
甲、乙两人分别从A，B两地同时出发、沿同一条路线相向匀速行驶，已知出发后3h两人相遇．乙的速度比甲快20km/h、相遇后乙再经1h到达A地．求甲、乙两人的速度．

共享时间:2024-01-28 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

23915. （2022•高新一中•二模）某校毕业班准备观看电影《长津湖》，由各班班长负责买票，每班人数都多于40人，票价每张30元，班长小王问售票员买团体票是否可以优惠，售票员说：40人以上的团体票有两种优惠方案可选择，方案一：全体人员可打8折；方案二：若打9折，有5人可以免票，班长小王思考一会儿说，我们班无论选择哪种方案要付的钱是一样的，你知道小王班有多少人吗？

共享时间:2022-03-14 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

23652. （2021•汇知中学•七上期末）根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定从2013年4月1日起对居民生活用电试行“阶梯电价”收费，具体收费标准见下表：

一户居民一个月用电量的范围	电费价格（单位：元/度）
不超过150度	a
超过150度的部分	b

2013年5月份，该市居民甲用电100度，交电费60元；居民乙用电200度，交电费122.5元．
（1）上表中，a= ，b= ；
（2）试行“阶梯电价”收费以后，该市一户居民2013年8月份平均电价每度为0.63元，求该用户8月用电多少度？

共享时间:2022-01-18 难度:4 相似度:1.25

解析

纠错

下载

组卷白板

23651. （2021•汇知中学•七上期末）为保证学生有足够的睡眠，政协委员于今年两会向大会提出一个议案，即“推迟中小学生早晨上课时间”，这个议案当即得到不少人大代表的支持．根据北京市教委的要求，学生小强所在学校将学生到校时间推迟半小时．小强原来7点从家出发乘坐公共汽车，7点20分到校；现在小强若由父母开车送其上学，7点45分出发，7点50分就到学校了．已知小强乘自家车比乘公交车平均每小时快36千米，求从小强家到学校的路程是多少千米？

共享时间:2022-01-18 难度:4 相似度:1.25

解析

纠错

下载

组卷白板

23591. （2020•高新一中•七上期末）某公园门票价格规定如下表：

购票张数	1-50张	51-100张	100张以上
单张票价	13元	11元	9元

某校七年级两个班共104人去游园，其中（1）班有40多人，不足50人，经估算，如果两个班各以班为单位购票，则一共应付1240元．问：
（1）两班各有多少学生？
（2）如果两班联合起来，作为一个团体购票，可省多少钱？

共享时间:2021-03-12 难度:4 相似度:1.25

解析

纠错

下载

组卷白板

zp@dyw.com

2024-10-22

初中数学 | 七年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2024-2025学年陕西省西安市雁塔区高新三中博雅班七年级（上）第一次月考数学试卷

更新:2024-10-22 09:35浏览量:36

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手