服务热线
搜题▪组卷
，且每粒种子是否发芽相互独立，对每一个坑而言，如果至少有两粒种子发芽，则不需要进行补播种，否则要补播种．（1）从n个坑中选两个坑进行观察，两坑不能相邻，有多少种方案？
种选法，
﹣n+1＝
种选法；
（
）3+
×
×（
）2＝
；
，
（
）3（1﹣
）n﹣3＝
（
）n，
，
（
）5＝
，
（
）6＝
，
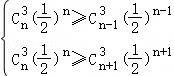．| 赔付金额（元） | 0 | 1000 | 2000 | 3000 | 4000 |
| 车辆数（辆） | 500 | 130 | 100 | 150 | 120 |
| 月工资/百元 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
，其中n＝a+b+c+d．
| P（K2≥k0） | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
，其中n＝a+b+c+d．
| P（K2≥k0） | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
dygzsxyn
2024-02-22
高中数学 | 高二上 | 解答题
纠错
收藏
下载
相似
组卷
解析