服务热线
搜题▪组卷
“赵爽弦图”是我国古代数学的骄傲，它巧妙利用面积关系证明了勾股定理，如图所示的“弦图”，是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较短直角边长为a,较长直角边长为b,若小正方形的面积为1，大正方形的面积为9，那么（a-b）2为 ．
ab＝9﹣1＝8，即2ab＝8，
“赵爽弦图”巧妙的利用面积关系证明了勾股定理．如图所示的“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，若AB=10，EF=2，则AH= ．
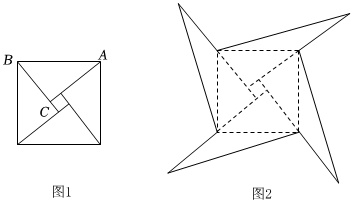如图，是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=12，BC=7，将四个直角三角形中边长为12的直角边分别向外延长一倍，得到如图所示的“数学风车”，则这个风车的外围周长是 ．
“赵爽弦图”是我国古代数学的骄傲，它巧妙利用面积关系证明了勾股定理．如图所示的“弦图”，是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较短直角边长为a,较长直角边长为b.若ab=6，小正方形的面积为9，则大正方形的面积为 ．
中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位．学习了勾股定理后，小明也绘制了的一幅“赵爽弦图”，如图①所示，已知他绘制的大正方形的面积是5，且图中四个全等的直角三角形与中间的小正方形恰好能拼成如图②所示的矩形，则矩形的周长是 ．
如图，我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理．若a=4，b=6，则图中正方形的边长为 ．
我国数学家赵爽在为天文学著作《周髀算经》作注解时，用4个全等的直角三角形和中间的小正方形拼成一个大正方形，这个图被称为“弦图”，它体现了中国古代数学的成就．如图，如果大正方形ABCD的面积是100，小正方形EFGH的面积是4，那么cos∠ADF= ．
我国是最早了解勾股定理的国家之一，东汉末年数学家刘徽在为《九章算术》作注中依据割补术而创造了勾股定理的无字证明“青朱出入图”，移动几个图形就直观地证明了勾股定理．如图，若CB=3，CG=4，则tan∠FEI= ．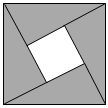
我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就，如图，由4个直角边分别是1和2的直角三角形拼成一个“弦图”地面，一个小球在如图所示的地面上自由滚动（小球大小不计），则小球停留在空白区域的概率是 ．
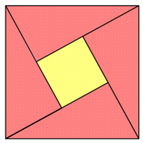如图，我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积是5，小正方形的面积是1，直角三角形的两直角边长分别是a、b（b＞a），则（a+b）2的值为 ．
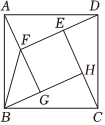我国最早对勾股定理进行证明的是数学家赵爽，他用4个全等的直角三角形和中间的一个小正方形组成了一个大正方形，如图所示，人们称这个图为“赵爽弦图”，连接BF，若S△ABF=12.5，AB-EF=6，则S正方形ABCD= ．
的值为 ．
公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，其中直角三角形中较大的锐角度数为α，若大正方形的面积为13，小正方形的面积为1，则sinα-cosα的值为 ．
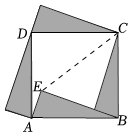清代数学家梅文鼎在《勾股举隅》一书中，用四个全等的直角三角形拼出正方形ABCD的方法证明了勾股定理（如图）．连结CE，若CE=5，BE=4，则正方形ABCD的边长为 ．
csyn@dyw.com
2023-05-16
初中数学 | | 填空题
纠错
收藏
下载
相似
组卷
解析
