服务热线
搜题▪组卷
＝1，
，
，
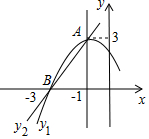如图，抛物线y1=ax2+bx+c（a≠0），其顶点坐标为A（-1，3），抛物线与x轴的一个交点为B（-3，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a-b=0，②abc＞0，③方程ax2+bx+c=3有两个相等的实数根，④抛物线与x轴的另一个交点是（1，0），⑤当-3＜x＜-1时，有y2＜y1．其中正确结论的个数是（ ）
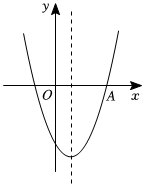如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（6，0），对称轴为直线x=2，结合图象分析如下结论：①abc＞0；②a+c＞b；③当x＜0时，y随x的增大而增大；④点D（x1，y1）、E（x2，y2）是函数图象上两点，若x1＜x2且x1+x2＜4，则y1＞y2．其中正确的有（ ）
A.当x1=x2＜1时，y1＜y2
C.当x1=x2＞1时，y1＜y2
B.当y1=y2＞n时，x1＞x2
D.当y1=y2＜n时，x1＞x2
A.没有交点
B.只有一个交点，且它位于y轴右侧
C.有两个交点，且它们均位于y轴左侧
D.有两个交点，且它们均位于y轴右侧
，其中正确的是（ ）
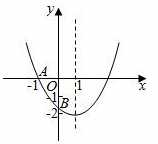
A.若点（a-1，y1）、（a+2，y2）在抛物线上，则y1＞y2
B.AB=a2-4
C.函数有最小值a-4
D.若抛物线过四个象限，则-2＜a＜2
A.x1=-1，x2=5
C.x1=1，x2=5
B.x1=-1，x2=-5
D.x1=1，x2=-5
csyn@dyw.com
2024-04-19
初中数学 | | 选择题
纠错
收藏
下载
相似
组卷
解析
