问题提出如图在锐角中如何作一个正方形使落在边上分别落在边上勤奋小组同学给出了如下作法画一个有三个顶点落在两边上的正方形连接并延长交于点过点作于点过作交于点过点作于点则四边形即为所求作的正方形受勤奋小组同学的启发创新小组同学认为可以在锐角中作出长与宽的比为的矩形使位于边上分别位于边上你

首页 > 试题列表 > 单题解析

23874. （2021•益新中学•九上期末）问题提出：如图，在锐角△ABC中，如何作一个正方形DEFG，使D，E落在BC边上，F，G分别落在AC，AB边上？
勤奋小组同学给出了如下作法：①画一个有三个顶点落在△ABC两边上的正方形HIJK；②连接BJ，并延长交AC于点F；③过点F作EF⊥BC于点E；④过F作FG∥BC，交AB于点G；⑤过点G作GD⊥BC于点D，则四边形DEFG即为所求作的正方形．
受勤奋小组同学的启发，创新小组同学认为可以在锐角△ABC中，作出长与宽的比为2：1的矩形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（1）你认为勤奋小组同学的作法正确吗？请说明理由；
（2）请你帮助创新小组同学在在锐角△ABC中，作出所有满足长与宽的比为2：1的矩形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．（在备用图中完成，不写作法，保留作图痕迹）
解决问题：
（3）在（2）的条件下，已知△ABC的面积为36，BC=12，求出矩形DEFG的面积． $德优题库$

共享时间:2021-02-07 难度:5

纠错

下载

相似

组卷白板

[考点]

相似三角形的判定与性质，矩形的判定与性质，正方形的判定与性质，四边形综合题，

[校正]

[答案]

（1）正确；
（2）图形见解析；
（3）18或．

[解析]

解：（1）正确．
理由：∵EF⊥BC，BC⊥GD，
∴∠FED＝∠EDG＝90°，
∵FG∥BC，
∴∠EFG＝180°﹣∠FED＝90°，
∴四边形DEFG是矩形，
∵四边形HIJK是正方形，
∴IJ＝KJ，KJ∥BC，
∴

，
∴GF＝EF，
∴四边形DEFG为正方形；
（2）如图1和图2，矩形DEFG为所作．

（3）如图3，作△ABC的高AM，交GF于点N，

∵△ABC的面积＝

BC•AM＝

×12×AM＝36，
∴AM＝6，
∵DE＝2DG，
设AN＝x，则MN＝6﹣x，DG＝MN＝6﹣x，DE＝GF＝2（6﹣x）＝12﹣2x，
∵GF∥BC，
∴△AGF∽△ABC，
∴

，
∴

，
解得x＝3，
∴DG＝6﹣x＝3，
∴DE＝2DG＝6，
∴矩形DEFG的面积＝6×3＝18，
同理，在矩形DEFG中，若DG＝2DE，可求出x＝

，
∴DG＝6﹣x＝

，DE＝

，
∴矩形DEFG的面积＝

＝

，
故矩形DEFG的面积为18或

．

[点评]

本题考查了"相似三角形的判定与性质,矩形的判定与性质,正方形的判定与性质,四边形综合题"，属于"压轴题"，熟悉考点是解题的关键。解题时注意数形结合思想与方程思想的应用，注意准确作出辅助线是解此题的关键．

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

考点说明

灰色代表去掉的考点，绿色代表未变动的考点，红色代表新增的考点

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

19254. （2016•西工大附中•模拟）问题探究：三角形的内接四边形指顶点在三角形各边上的四边形．
（1）如图1，△ABC中，AB＝AC，正方形MNFE的顶点M、E在BC上，顶点N在AB上，请以点B为位似中心，作△ABC的内接正方形．（不写作法）．
（2）如图2，△ABC中，BC＝12，∠B＝45°，AD⊥BC于点D，AD＝8，请以点D为位似中心，作△ABC的内接正方形，并求出所作正方形的面积（不写作法）．
问题解决
（3）如图3，将（2）中的△ABC翻折得到四边形ABEC，对角线AE、BC相交于点D，请以点D为位似中心作正方形MNPQ，使得点M、N、P、Q在四边形ABEC的各边上．
要求：①写出作法，证明四边形MNPQ是正方形；
②求出正方形MNPQ的面积．

共享时间:2016-06-06 难度:5 相似度:1.5

解析

纠错

下载

组卷白板

287660. （2019•益新中学•三模）问题提出
（1）如图1点C为线段AB外一点，且AB=8，AC=7，那么线段BC长的最大值是，最小值是．
问题探究
（2）如图2点C为线段AB外一点，已知AB=8，AC=7，点D，点E分别是△CAB外两点且△DAC是以AC为斜边的等腰直角三角形，△CBE是以CE为斜边的等腰直角三角形，连接AE、BD，试探究线段AE的最大值？
问题解决
（3）某湿地公园利用河流荒滩建立野生动物园，经过测量湿地是一大块四边形ABCD，其中BA=BC，∠ABC=90°．边AD长24千米，CD长18千米，为了方便照顾好园区的动物，规划部门要求要经过BD修建一条笔直的公路且最长的公路，你能帮助计算出最长公路和此时动物园占地面积吗？ $德优题库$

共享时间:2019-04-08 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

288081. （2018•爱知中学•二模）知识运用：
（1）如图1，已知正方形ABCD，请用直尺和圆规作以BC为边的等边三角形BCP，使得点P在正方形ABCD的内部（保留作图痕迹）；
知识探究：
（2）如图2，小明画出了图1的正方形ABCD和等边三角形PBC．他发现，在正方形ABCD中把△PBC经过图形变化（旋转后放大），可以得到图2中的更大的等边三角形．请你通过合理的图形变化，在图3的正方形纸片中画出面积最大的等边三角形BEF（点E、F不能在正方形外），当图3正方形ABCD的边长为1时，求等边三角形BEF的最大边长．
知识应用：
（3）某单位现有一块建筑用地，其形状为Rt△ABC（如图3），其中∠A=90°，AC=3，AB=4．因工作需要，单位要求承建方将此三角形ABC用地扩建成一个正方形用地（周围有足够的用地），要求原来位于A、B、C三个顶点的三棵树在正方形的内部或边上．为了节省费用，建筑方想让这个正方形尽可能的小，请你在图中画出扩建后满足条件的面积最小的正方形，并求出该正方形的最小面积．
$德优题库$

共享时间:2018-03-21 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

274880. （2024•西工大附中•九模）（1）如图①，在矩形ABCD中，AB＝6，BC＝8，点P在边BC上．连接AP，过点P作PQ⊥AP．求AQ的最小值；
（2）如图②，矩形ABCD是某公园示意图，其中AB＝600米，BC＝800米．为了进一步改善人居环境，现需要对公园进行改扩建．根据现场勘察情况，边DC的外边有一片空地可以扩建．设计部门打算把扩建部分设计为直角三角形，即Rt△CDE，且∠CED＝90°，同时要在扩建后的五边形公园ABCED中的边BC上开一个门F，使得点F到点A、点E的距离相等且∠AFE＝90°．试问这样的设计能否实现？若能，求出扩建部分△CDE的面积及点F到点B的距离；若不能，请说明理由．

共享时间:2024-06-15 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

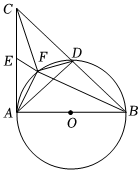284271. （2023•铁一中学•四模） $德优题库$ 如图，AB为⊙O的直径，AC是⊙O的切线，且AC=AB，连接CB交⊙O于点D，E为AC的中点，连接BE交⊙O于点F，连接AD，CF，DF，AF．
（1）求证：CE²=EF•EB；
（2）若DF=1，求AF的长．

共享时间:2023-04-24 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

284325. （2023•铁一中学•二模）现有一块矩形板材ABCD，AB=4，AD=6，点E为边BC上一点，连接AE，过点E在矩形板材上作EF⊥AE，且EF=AE．
（1）如图1，若点F恰好落在边CD上，则线段CF的长为；
（2）如图2，连接CF，求线段CF长度的最小值；
（3）如图3，连接DF，工人师傅能否在这块矩形板材上裁出面积最小的四边形AEFD？若能，请求出四边形AEFD面积的最小值；若不能，请说明理由．
$德优题库$

共享时间:2023-03-16 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

284789. （2022•高新一中•八模）如图，在矩形ABCD中，AB＝3cm，AD＝

cm．动点P在边AB上从点A向点B运动，速度为1cm/s；过点P作线段PQ与射线DC相交于点Q，且∠PQD＝60°，连接PD，BD．设点P的运动时间为x（s），△DPQ与△DBC重合部分图形的面积为y（cm²）．
（1）当x＝　　 s时，点Q与点C重合；
（2）①求y关于x的函数关系式，并写出自变量x的取值范围；
②在点P的运动过程中，是否存在y的最大值，若存在，请求出最大值；若不存在，请说明理由．

共享时间:2022-06-11 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

285895. （2022•交大附中•一模）（1）如图①，点A、点B在直线l同侧，请你在直线l上找一点P，使得AP+BP的值最小；（不需要说明理由）
（2）如图②，∠AOB＝60°，点P为∠AOB内一定点，OP＝5，点E，F分别在OA，OB上，△PEF的周长是否存在最小值？若存在，请求出最小值，若不存在，请说明理由；
（3）如图③，已知四边形OABC中，∠A＝∠C＝90°，∠B＝150°，BC＝2，OC＝

，点H为OA边上的一点且OH＝4，点P，F分别在边AB，OC上运动，点E在线段OH上运动，连接EF，EP，PF，△EFP的周长是否存在最小值？若存在，请求出△EFP周长最小值和此时OE的长，若不存在，请说明理由．

共享时间:2022-03-13 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

287303. （2020•师大附中•九模）问题提出
（1）如图①，点A在直线m上，点P在直线m外，请用尺规在直线m上找一点B，使得∠APB=60°（只作出满足条件一个图形即可）；
（2）如图②，在四边形ABCD中，∠ABC=∠ADC=90°，AD=CD，对角线BD=10，求四边形ABCD的面积．
问题解决
（3）如图③，园林规划局想在正六边形草坪一角∠BOC内改建一个小型的儿童游乐场OMAN，其中OA平分∠BOC，OA=100米，∠BOC=120°，点M、N分别在射线OB和OC上，且∠MAN=90°，为了尽可能的少破坏草坪，要使游乐场OMAN面积最小．你认为园林规划局的想法能实现吗？若能，请求出游乐场OMAN面积的最小值；若不能，请说明理由．
$德优题库$

共享时间:2020-06-15 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

287386. （2020•铁一中学•七模）问题提出：
（1）如图①，矩形ABCD中，AD＝6．点E为AD的中点．点F在AB上_△EFC＝　　．
问题探究：
（2）如图②．已知矩形ABCD纸片中．AB＝9，AD＝6，点P是CD边上一动点．点Q是BC的中点．将△ADP沿着AP折叠，将△QCP沿着PQ折叠．在纸片上点C的对应点是C′．请问是否存在这样的点P．使得点P、D'、C′在同一条直线上？若存在，求出此时DP的长度．若不存在
问题解决：
（3）某精密仪器厂接到生产一种特殊四边形金属部件的任务．部件要求：如图③，四边形ABCD中，AB＝4厘米，BC⊥CD．且BC＝

CD．在满足要求和保证质量的前提下，已知这种金属材料每平方厘米造价50元．请问这种四边形金属部件每个的造价最低是多少元？（

≈1.73）

共享时间:2020-06-06 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

882. （2013•陕西省•真题）问题探究：
（1）请在图①中作出两条直线，使它们将圆面四等分；
（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M）使它们将正方形ABCD的面积四等分，并说明理由．
问题解决：
（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．

共享时间:2013-11-18 难度:3 相似度:1.25

解析

纠错

下载

组卷白板

191817. （2023•经开一中•九上二月）问题提出
（1）如图1，在Rt△ABC中，CA=CB，∠ACB=90°，P为此三角形内的一点，且PB=1，PC=2，PA=3，将△CPB绕点C沿顺时针方向旋转90°至△CQA，则∠BPC的度数为．
问题探究
（2）如图2，在四边形ACBD中，∠ACB=∠ADB=90°，AC=BC，探究线段AD、BD、CD之间的数量关系并写出解答过程．
问题解决
（3）如图3是某公园内“少儿活动中心”的设计示意图，已知四边形ACBD中，∠ACB=∠ADB=90°，AC=BC，AB=70m,DC平分∠ADB交AB于点P，PE⊥AD于点E，PF⊥BD于点F．按设计要求，四边形PEDF内部为室内活动区，阴影部分是户外活动区，若AP的长为30m,则阴影部分的面积为 m²．
$德优题库$

共享时间:2023-12-22 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

284740. （2022•高新一中•七模）问题提出：
（1）如图1，△ABC中，点D是边AB上一点，

＝

，过点D分别作DE∥AC，DF∥BC，交BC、AC于点E、F，则

＝　　，

＝　　；
问题解决：
（2）如图2，有一块四边形木板ABCD，对角线AC⊥BD，AC＝80cm，BD＝60cm．现要在四边形ABCD木板中裁出一块Rt△EFG木板，∠FEG＝90°，三个顶点分别在边AB、BC、AD上，其中EG∥BD．
①设EG＝x，请用含x的代数式表示EF的长；
②问是否存在面积最大的Rt△EFG，若存在，求出此时EG的长；若不存在，请说明理由．

共享时间:2022-06-02 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

284735. （2022•高新一中•七模）北京冬奥会的首钢滑雪大跳台是世界上首个永久性的单板大跳台，其优美的造型，独特的设计给全球观众留下深刻的印象．现将大跳台抽象成如图的简图，CD表示助滑区，Rt△DEH表示起跳台，EB表示着陆坡．已知∠EBF＝30°，从点D处测得C处的仰角等于∠HDE的度数，CA＝52m，DE＝10m，HE＝5m，AB＝110m，DE∥BF，CA、DG、EM都垂直于BF．求起跳台高度HM的值．（结果保留整数，

≈1.73）

共享时间:2022-06-02 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

212398. （2025•交大附中•一模）数学兴趣小组接到一项任务，需要让他们在一个矩形板材上裁剪出一个符合要求的四边形部件，任务具体如下：
【任务一】在如图的矩形板材ABCD中，AB=40cm,AD=80cm,取AD边上一点E，ED=30cm,请你帮数学兴趣小组在BC边上找一点F，连接EF，使得线段EF平分矩形ABCD的面积，则线段EF的长为 cm.
【任务二】在完成任务一后，取线段EF的中点O，点M和点N是线段EF上两点，且OM=ON=10cm（M在O点上方，N在O点下方），要求兴趣小组在线段BC上找一点P，连接PM和PN，使得∠MPN角度最大，请帮兴趣小组计算，当∠MPN角度最大时，sin∠MPN的值．
【任务三】在任务二的结论下，线段EF的左侧是否存在点Q，连接QM和QN，使得∠MQN=∠MPN，且满足四边形QNPM的面积最大，若存在，求出四边形QNPM的面积最大值；若不存在，请说明理由．
$德优题库$

共享时间:2025-03-13 难度:1 相似度:1.25

解析

纠错

下载

组卷白板

yxzx2021

2021-02-07

初中数学 | 九年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2020-2021陕西省西安市莲湖区益新中学九年级上期末数学试卷

更新:2021-02-07 05:27浏览量:1053

微信扫码立即登录

AI助手

登录

注册

微信扫码立即登录

AI助手