服务热线
搜题▪组卷
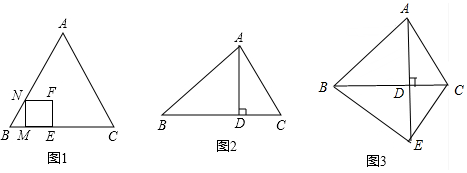
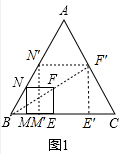
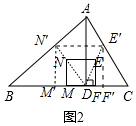
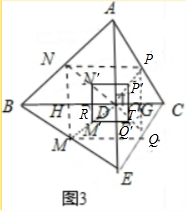
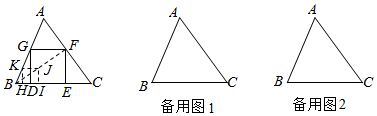
 小延想要测量学校教学楼AB的高度,他站在N点处时,视线通过旗杆DE的顶端与顶楼的窗子下沿C重合,他向前走到点G处时,视线通过旗杆DE的顶端与楼顶A重合,已知小延的眼睛与地面的距离MN=FG=1.6米,NG=2米,GE=6米,BE=8米,AC=3米,MN、FG、DE、AB均与地面垂直,且在同一平面内,请你根据以上数据计算教学楼AB的高度.
小延想要测量学校教学楼AB的高度,他站在N点处时,视线通过旗杆DE的顶端与顶楼的窗子下沿C重合,他向前走到点G处时,视线通过旗杆DE的顶端与楼顶A重合,已知小延的眼睛与地面的距离MN=FG=1.6米,NG=2米,GE=6米,BE=8米,AC=3米,MN、FG、DE、AB均与地面垂直,且在同一平面内,请你根据以上数据计算教学楼AB的高度.






xgd513
2016-06-06
初中数学 | | 解答题