服务热线
搜题▪组卷
，且△ABC有两解，则b的取值范围为[3，3
]
，3
）
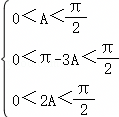，所以△ABC的外接圆的直径2R＝
＝2
，所以R＝
，
）2＝3π，选项A正确，
＜3＜b，解得3＜b＜3
，∴B错误，
＝
，得
＝
，即c＝2acosA＝6cosA，
，所以
＜A＜
，
，3
），故选项C正确，
，故cosC＝
，sinC＝
，
×
＝
，
＝
，a＝3可得：c＝
，b＝2
，则a+b+c＝3+3
，
bcsinA＝
×2
×
×
＝
，
＝
＝
，
cr＝
×
×
＝
，故D正确．
A.．若acosA＝bcosB，则△ABC是等腰三角形
B.在锐角△ABC中，不等式sinA＞cosB恒成立
C.若tanA+tanB+tanC＞0，则△ABC为锐角三角形
D.．若
，则cosAcosC的取值范围是
dygzsxyn
2023-04-26
高中数学 | 高一下 | 多选题
纠错
收藏
下载
相似
组卷
解析
