[答案]
(1)x2=4y;
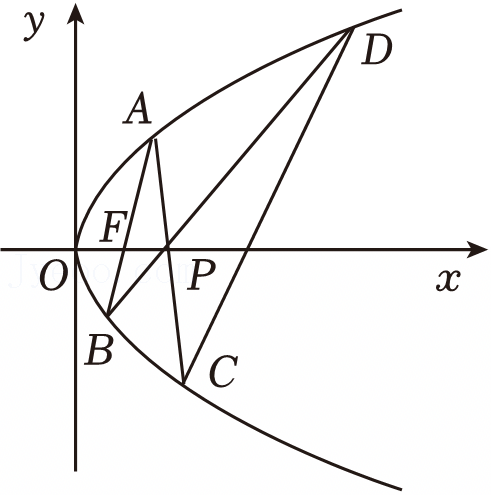
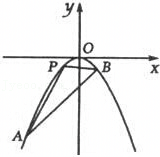
(2)证明:设N(x0,y0)是直线l:y=x﹣4上任意一点,过N作抛物线的切线分别为l1,l2,切点分别为A(x1,y1),B(x2,y2),则l1的方程为:xx1=2(y+y1) ①
l2的方程为:xx2=2(y+y2) ②
因为l1l2都过N(x0,y0)点,所以有x0x1=2(y0+y1),③
x0x2=2(y0+y2),④
③和④表示A,B两点均在直线x0x=2(y0+y),
即直线AB的方程为:x0x=2(y0+y),又y0=x0﹣4,
所以:x0x=2(x0﹣4+y),
所以直线AB的方程可化为:x0(x﹣2)+(﹣2y+8)=0,x0(x﹣2)﹣2(y﹣4)=0
即直线AB恒过(2,4)点.
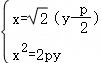 .整理得:2y2﹣4py+
.整理得:2y2﹣4py+