服务热线
搜题▪组卷
x+1分别与x轴、y轴交于点A、B，直线CD：y=x+b分别与x轴、y轴交于点C、D，直线AB与CD相交于点P，S△ABD=2．求：
分别与x轴、y轴交于点A、B，
|BD|•|OA|＝2而|OA|＝2
，
|xP|＝6
|yP|）＝
×3×（1+3）＝6．（9分）
，求点P的坐标．
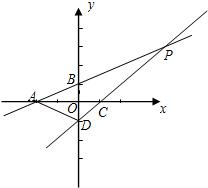
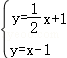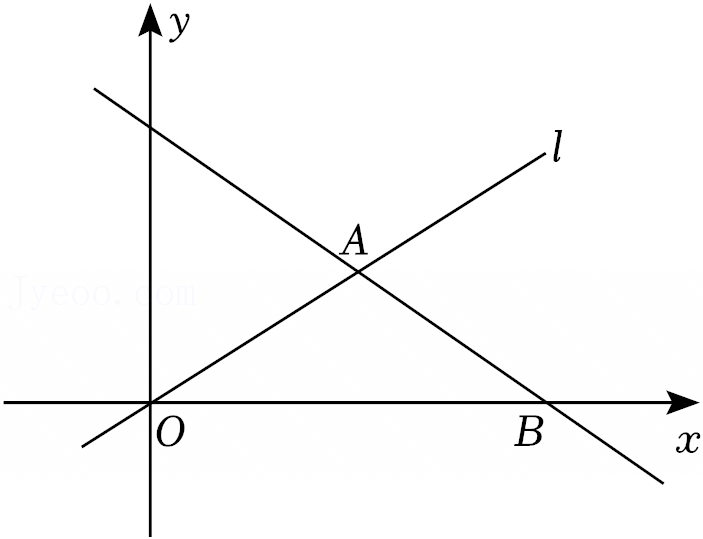
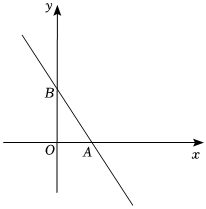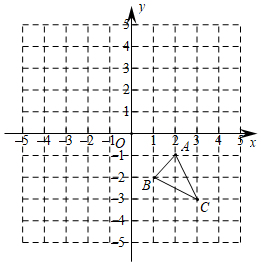
如图，在平面直角坐标系中，已知直线y=kx+3经过点（4，-3），与x轴交于点A，与y轴交于点B，直线上有一个点M（1，n）．
如图，公园一角有一片空地，记为△ABC，公园负责人计划在这片空地中种上红色和黄色的月季花，为体现美观性和整体性，请你帮园丁师傅在BC上找一点D，使得S△ABD=S△ACD．（不写作法，保留作图痕迹）
| 车型 | 目的地 | ||
| A村（元/辆） | B村（元/辆） | ||
| 大货车 | |||
| 800 | 900 | ||
| 小货车 | 400 | 600 | |
gxyz515
2021-11-18
初中数学 | 八年级上 | 解答题
纠错
收藏
下载
相似
组卷
解析
如图，在平面直角坐标系中，点A（0，5），B（-1，2），C（3，2），直线l经过点A，并将△ABC分成面积相等的两部分，求直线l的表达式．
如图，已知四边形ABCD，点E在边CD上，且EC=BC．请用尺规作图法，在边AD上求作一点P，使△PCE与△PCB面积相等．（保留作图痕迹，不写作法）
如图，在△ABC中，AD是BC边上的中线，请用尺规作图法在AC边上作一点P，使得S△ABC=4S△ADP．（保留作图痕迹，不写作法）
如图，在△ABC中，点D为AB边的中点，请用直尺和圆规在AC边上求作一点E，使得S△BCE=S△BCD．（不写作法，保留作图痕迹）
如图，在四边形ABCD中，AB=BC，AD＞DC，在AD上作一点P，使得S△ABP=S△CBP（要求：尺规作图，不写作法，保留作图痕迹）．
如图，已知四边形ABCD，点E在边CD上，且EC=BC．请用尺规作图法，在边AD上求作一点P，使△PCE与△PCB面积相等．（保留作图痕迹，不写作法）
