服务热线
搜题▪组卷
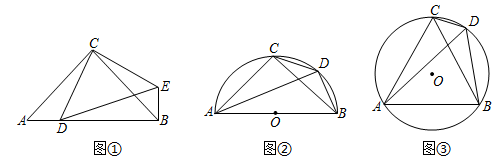
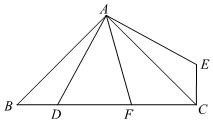
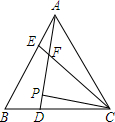 已知:如图,△ABC为等边三角形,AE=BD,AD,CE相交于点F.
已知:如图,△ABC为等边三角形,AE=BD,AD,CE相交于点F.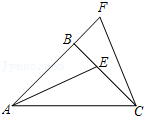
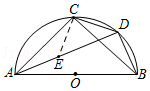
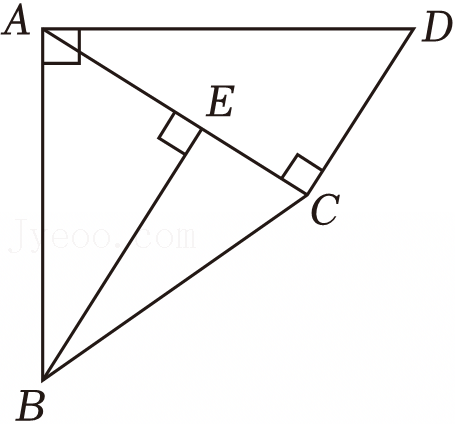
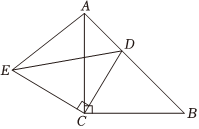 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
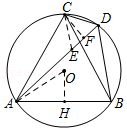
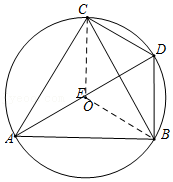
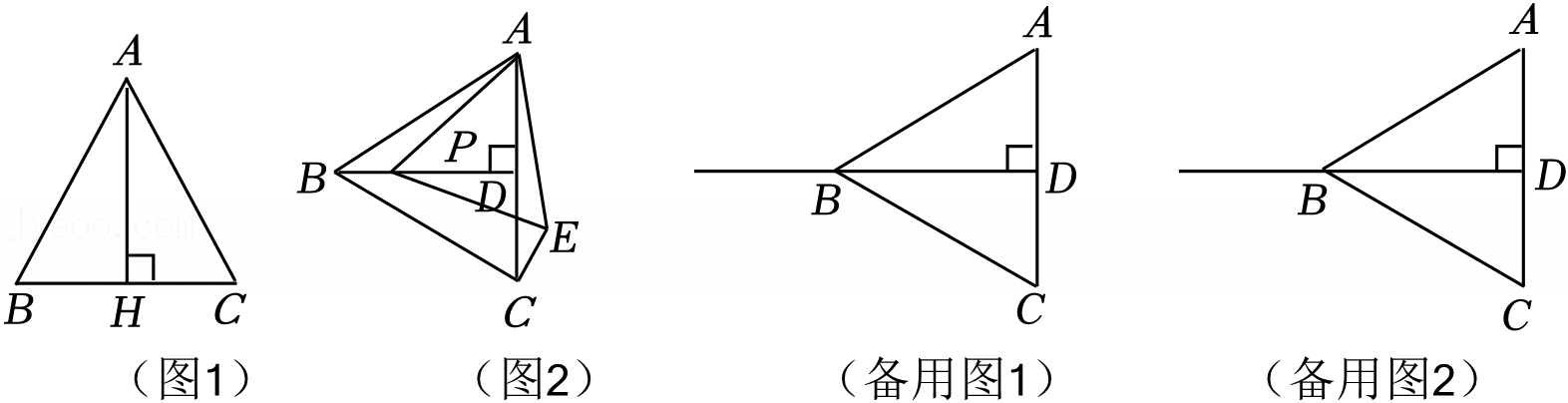
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证: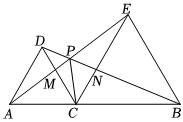 如图所示,A、C、B三点共线,△DAC与△EBC都是等边三角形,AE、BD相交于点P,且分别与CD、CE交于点M,N.
如图所示,A、C、B三点共线,△DAC与△EBC都是等边三角形,AE、BD相交于点P,且分别与CD、CE交于点M,N.
dysx2021
2021-07-25
初中数学 | | 解答题