服务热线
搜题▪组卷
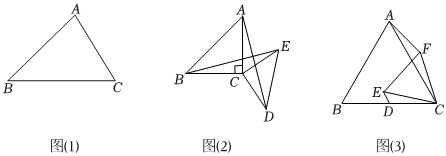
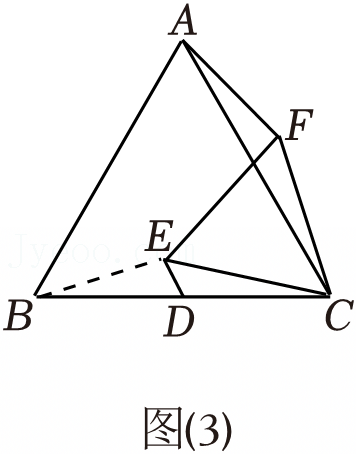
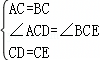 ,
,
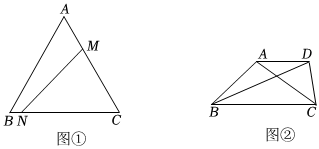
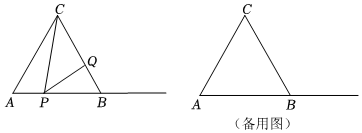
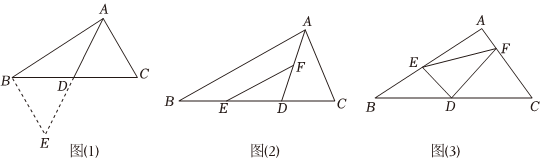
 如图所示,在等边△ABC中,AB=BC=AC=6cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;点Q从点C出发,沿CB方向匀速运动,速度为2cm/s,连接PQ,AQ.设运动时间为t秒(0<t<3),请回答:
如图所示,在等边△ABC中,AB=BC=AC=6cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;点Q从点C出发,沿CB方向匀速运动,速度为2cm/s,连接PQ,AQ.设运动时间为t秒(0<t<3),请回答: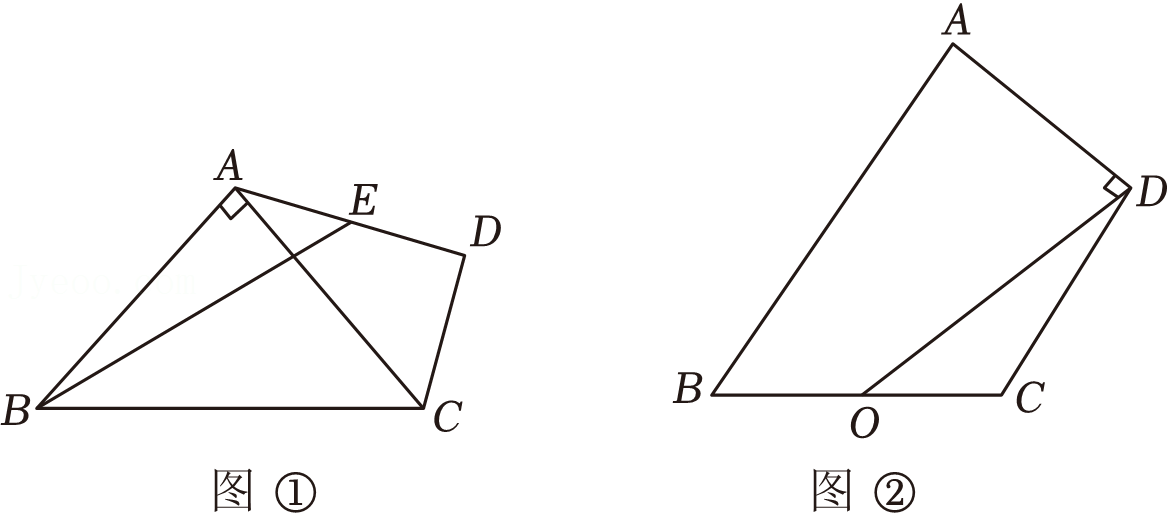

dyczsxyn
2024-05-10
初中数学 | 七年级下 | 解答题