问题探究如图等边的边长为分别是边上的点且满足求的长问题解决如图道路长为米的一侧是一片足够大的学校实践基地现计划在这片基地上规划一个四边形花园按设计要求点为出入口点为休息厅现准备过点规划两条小路与且满足米为了满足设计的需要要使两条小路长度之和最大请问是否存在符合要求的两条小路若存在求出两条小路长度之和即的

首页 > 试题列表 > 单题解析

212424. （2025•交大附中•四模）问题探究
（1）如图①，等边△ABC的边长为6，M，N分别是边AC，BC上的点，且满足AM=2，∠CMN=75°，求BN的长；
问题解决
（2）如图②，道路长为120米的BC一侧是一片足够大的学校实践基地，现计划在这片基地上规划一个四边形花园ABCD，按设计要求：点A，B，C，D为出入口，点P为休息厅，现准备过点P规划两条小路AC与BD，且满足∠BPC=120°，AD∥BC，AD=60米，为了满足设计的需要，要使两条小路长度之和最大，请问是否存在符合要求的两条小路？若存在，求出两条小路长度之和（即AC+BD）的最大值，若不存在，请说明理由．
$德优题库$

共享时间:2025-04-27 难度:1

纠错

下载

相似

组卷白板

[考点]

三角形综合题，

[校正]

[答案]

（1）4﹣2

；

（2）存在，为

米．

[解析]

解：（1）如图，过点M作MD⊥BC，垂足为D，

∵AC＝6，AM＝2，
∴CM＝4，
∵△ABC是等边三角形，
∴∠ACB＝60°，
∴在Rt△MDC中，CD＝2，

，
∵在△MNC中，∠CMN＝75°，
∴∠MND＝45°，
∴

，
∴

；
（2）存在，如图，过点D作DF∥AC交BC的延长线于点F，

∵AD∥BC，DF∥AC，
∴四边形ACFD是平行四边形，
∴CF＝AD＝60，DF＝AC，∠BDF＝∠BPC＝120°，
∴BF＝BC+CF＝120+60＝180，
延长BD至点E，使DE＝DF，过点B作BH⊥EF交EF的延长线于点H，
∴∠EDF＝180°﹣∠BDF＝180°﹣120°＝60°，
∵DE＝DF，
∴△DFE是等边三角形，
∴∠BEH＝60°，
∴

，
∵BF≥BH，
∴

，
∴

，
∵AC+BD＝DF+BD＝DE+BD＝BE，
∴

，
即当点F与点H重合时，AC+BD取得最大值，最大值为

，
∴存在符合要求的两条小路，两条小路长度之和（即AC+BD）的最大值为

米．

[点评]

本题考查了"三角形综合题，"，属于"基础题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

考点说明

灰色代表去掉的考点，绿色代表未变动的考点，红色代表新增的考点

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

290043. （2016•铁一中学•二模）问题提出
（1）如图1，AB∥DC，试在射线DC上找一点E_{四边形ABCD}＝S_△BDE，并指出四边形ACEB是何种四边形．
（2）如图2，Rt△ABC中，∠A＝90°，AC＝4，将△ABC绕C点顺时针旋转60°得到△A'B'C
（3）如图3，Rt△ABC中，∠A＝60°

，点D在BC边上，且BD＝2，点E、F在AC边上，线段DE与线段GF交于点O，∠EOF＝60°，试求出四边形DGEF面积的最大和最小值．

共享时间:2016-03-27 难度:1 相似度:2

解析

纠错

下载

组卷白板

196900. （2024•交大附中•七下期末）小明同学在学习完全等三角形后，发现可以通过添加辅助线构造全等三角形来解决问题．
（1）如图（1），AD是△ABC的中线，且AB＞AC，延长AD至点E，使ED=AD，连接BE，可证得△ADC≌△EDB，其中判定两个三角形全等的依据为．
（2）如图（2），在△ABC中，点E在BC上，且DE=DC，过E作EF∥AB，且EF=AC．求证：AD平分∠BAC．
（3）如图（3），在△ABC中，∠A=90°，D为BC中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．若BE=1.8，CF=2.4，求EF的长度． $德优题库$

共享时间:2024-07-09 难度:1 相似度:2

解析

纠错

下载

组卷白板

198585. （2023•莲湖区•八下期中）在边长为10的等边△ABC中，点P从点B出发沿射线BA移动，同时点Q从点C出发沿线段AC的延长线移动，点P、Q移动的速度相同，PQ与直线BC相交于点D．
$德优题库$
（1）如图①，当点P为AB的中点时，
（Ⅰ）求证：PD=QD；
（Ⅱ）求CD的长；
（2）如图②，过点P作直线BC的垂线，垂足为E，当点P、Q在移动的过程中，试确定BE、CD的数量关系，并说明理由．

共享时间:2023-05-12 难度:1 相似度:2

解析

纠错

下载

组卷白板

198437. （2022•爱知中学•八上期中）（1）如图①，△ABC与△ADE均是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，线段BD、CE交于点F．则∠DFE＝　　．
（2）如图②，△ABC是等腰直角三角形，∠BAC＝90°，AB＝AC，延长BC至点D，使

，以AD为直角边在AD的左侧作等腰直角△ADE，使得AD＝AE＝6，∠DAE＝90°，连接CE，求线段CE的长．
（3）如图③，△ABC为等腰直角三角形，∠BAC＝90°，AB＝AC，在AC的左侧作△ACD，使得AD＝6，∠ADC＝45°，

，连接BD，求线段BD的长．

共享时间:2022-11-23 难度:1 相似度:2

解析

纠错

下载

组卷白板

198341. （2023•新城区•八上期中）问题情境：老师在黑板上出了这样一道题：直线l同旁有两个定点A，B，在直线l上是否存在点P，使得PA+PB的值最小？
小明的解法如下：如图1，作点A关于直线l的对称点A'，连接A'B，则A'B与直线l的交点即为P，且PA+PB的最小值为A'B．
问题提出：
（1）如图2，等腰Rt△ABC的直角边长为4，E是斜边AB的中点，P是AC边上的一动点，求PB+PE的最小值．
问题解决：
（2）如图3，为了解决A，B两村的村民饮用水问题，A，B两村计划在一水渠上建造一个蓄水池M，从蓄水池M处向A，B两村引水，A，B两村到河边的距离分别为AC=3千米，BD=9千米，CD=9千米．若蓄水池往两村铺设水管的工程费用为每千米15000元，请你在水渠CD上选择蓄水池M的位置，使铺设水管的费用最少，并求出最少的铺设水管的费用．
$德优题库$

共享时间:2023-11-15 难度:1 相似度:2

解析

纠错

下载

组卷白板

198088. （2023•师大附中•九上期中）如图1，在△ABC中，AB＝AC，∠BAC＝α，D，E分别为AB，BC边上一点，连接DE，且BD＝DE，将△ABC绕点B在平面内旋转．
（1）观察猜想
若α＝60°，将△ABC绕点B旋转到如图2所示的位置，则

的值为　　．
（2）类比探究
若α＝90°，将△ABC绕点B旋转到如图3所示的位置，求

的值．
（3）拓展应用
若α＝90°，D为AB的中点，AB＝6，当AD⊥BE中，请求出CE的值．

共享时间:2023-11-30 难度:1 相似度:2

解析

纠错

下载

组卷白板

198016. （2024•交大附中•八上期中）【方法归纳】同学们，我们在学完勾股定理的证明后发现：运用“同一图形的面积的不同表示方式”可以用来探究线段之间的关系．今天，我们来尝试用这种方法来解决以下问题．
（1）【小试牛刀】如图1，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，BD⊥AC于点D，则BD= ．
（2）【学有所用】如图2，△ABC中，AB=AC=8，S_△ABC=20，M是底边BC上的任意一点，且M到AB、AC的距离分别为h₁、h₂．请问：h₁+h₂是定值吗？如果是，求出这个值；如果不是，说明理由．
（3）【拓展升华】在平面直角坐标系中，三个点A（-6，0），B（4，0），C（0，8），M为直线BC上一点，且到AC的距离为3．求点M的坐标．
$德优题库$

共享时间:2024-11-13 难度:1 相似度:2

解析

纠错

下载

组卷白板

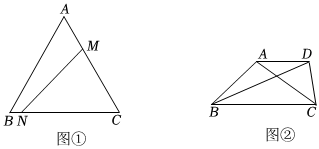
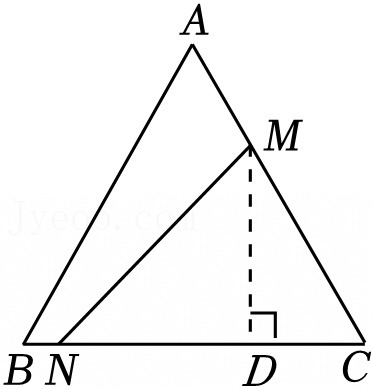
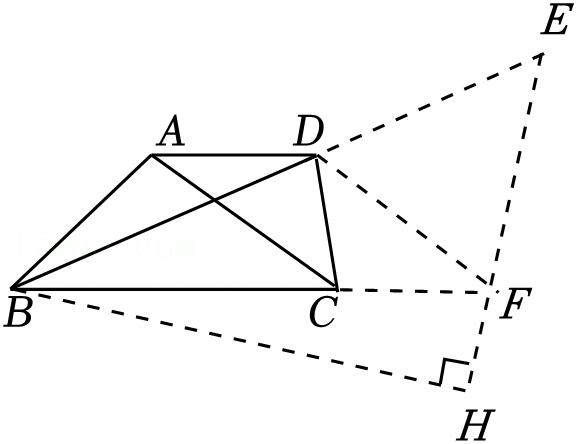
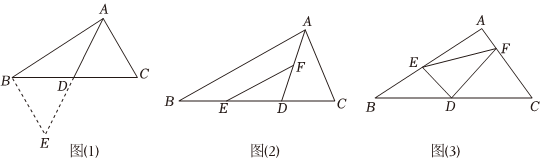
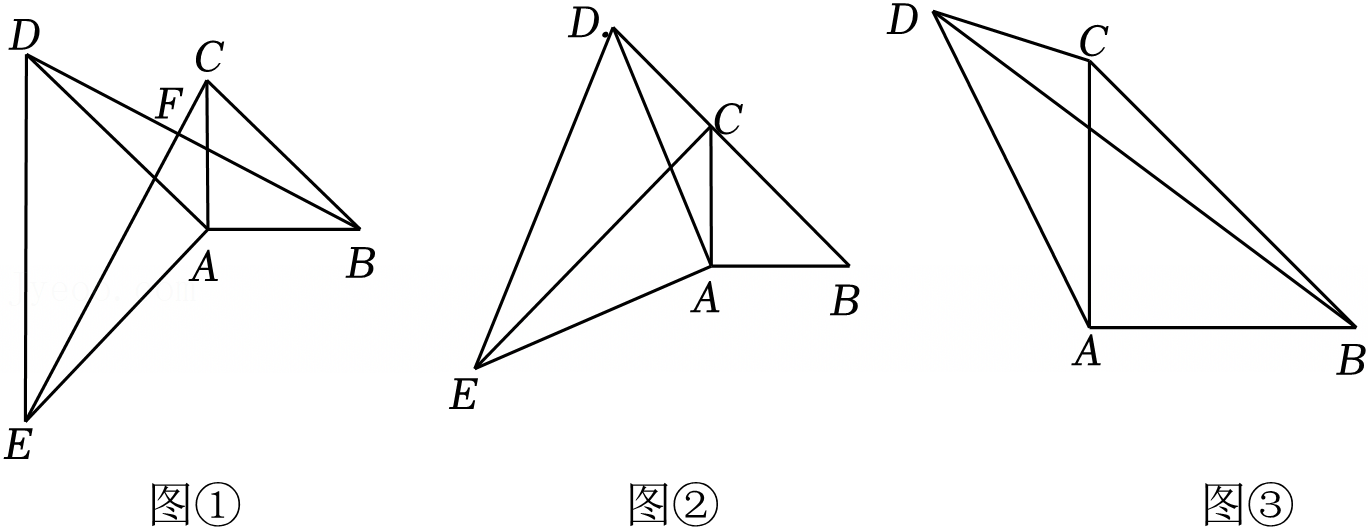
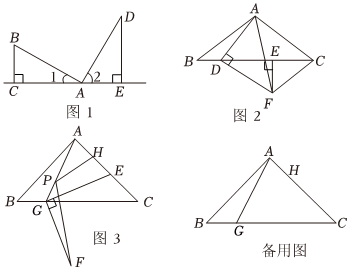
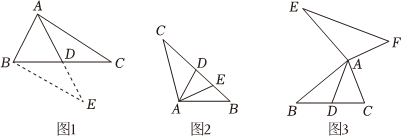
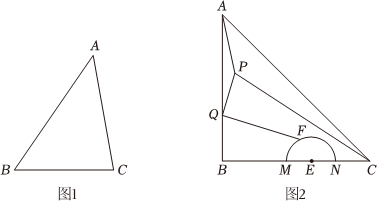
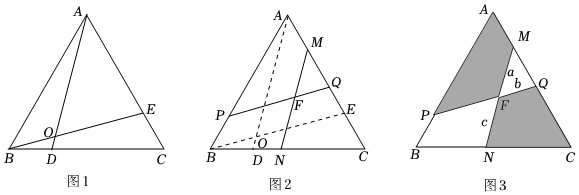
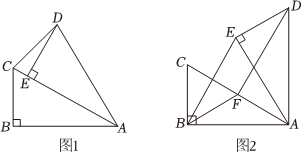197547. （2024•高新陆港•九上期中） $德优题库$ 在Rt△ABC中，∠ABC=90°，∠BAC=30°，将△ABC绕点A顺时针旋转一定的角度α后得到△AED，点B，C的对应点分别是E，D．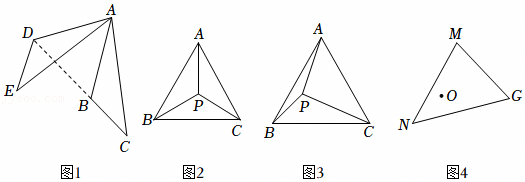
（1）如图1，当点E恰好在AC上时，求∠CDE的度数；
（2）如图2，若α=60°，点F是边AC的中点，试说明四边形BFDE是平行四边形；
（3）若BC=4，连接CE，CD．在旋转的过程中，△CDE的面积是否存在最大值？若存在，请求出其面积最大值；若不存在，请说明理由．

共享时间:2024-11-22 难度:1 相似度:2

解析

纠错

下载

组卷白板

197399. （2024•高新三中•八下期中）根据材料回答下列小题
（1）【操作发现】如图1，将△ABC绕点A顺时针旋转60°，得到△ADE，连接BD，则△ABD是　　三角形
（2）【类比探究】如图2，在等边三角形ABC内任取一点P，连接PA，PB，PC，求证：以PA，PB，PC
的长为三边必能组成三角形．
（3）【解决问题】如图3，在边长为

的等边三角形ABC内有一点P，∠APC＝90°，∠BPC＝120°求△APC的面积．
（4）【拓展应用]如图4是M，N，G三个村子位置的平面图经测量MN＝6km，∠M＝75°，MG＝4

km，区管委会想在△MNG内建污水处理厂，为了快捷、环保和节约成本，要使得线段OM、ON、OG之和最短，试求OM+ON+OG的最小值（污水处理厂与所在道路之间的距离、路宽均忽略不计了．

共享时间:2024-05-13 难度:1 相似度:2

解析

纠错

下载

组卷白板

196459. （2024•爱知中学•七下期末）问题发现：学习三角形全等的知识时，小明发现重合两个等腰直角三角形的顶点会产生一对新的全等三角形．
如图1，Rt△ABC中，∠BAC=90°，AB=AC，点D在边BC上，连接AD，以AD为边作△ADE，使∠DAE=90°，AD=AE，请连接图中标有字母的点，补全图形，直接写出一对全等三角形和∠BCE的度数．
问题探究：小明想，如果将图中的等腰直角三角形换成等边三角形，那么这组全等三角形是否还存在？
如图2，△ABC和△ADE是等边三角形，点B，D，E在同一直线．
（1）证明：△ABD≌△ACE．
（2）探索线段BE，AE，CE三者间的数量关系，写出结论并说明理由．
问题拓展：经过上面的探究，小明联想到几天前一道不会的题，请你帮小明再想一想，是否有新的发现．
如图3，边长为a的等边△ABC中，D是AC中点，BD=b,E是线段BD上一动点，连接AE，在AE右侧作等边△AEF，连接FD，求△AFD周长的最小值（用含a,b的代数式表示），并直接写出取最小值时∠AFD的度数．
$德优题库$

共享时间:2024-07-21 难度:1 相似度:2

解析

纠错

下载

组卷白板

199046. （2021•师大附中•七下期末）初步探索
在△ABC中，∠BAC＝90°，AB＝AC，∠ABC＝45°，点D是线段BC上的一个动点（不与点B重合）．DE⊥BE于点E，∠EBA＝

∠ACB，DE与AB相交于点F．

（1）当点D与点C重合时（如图①），∠EBA＝　　 °；
（2）灵活应用：在（1）的条件下，试探究线段BE与DF的数量关系，并说明理由；
（3）问题解决：当点D与点C不重合时（如图②），你认为（2）中线段BE与DF的数量关系是否仍然成立？直接写出你的猜想．

共享时间:2021-07-14 难度:1 相似度:2

解析

纠错

下载

组卷白板

196335. （2024•高新一中•七下期末）（1）【特例感知】如图1，∠BAD=90°，AB=AD，BC⊥AC于点C，DE⊥AC于点E．A、C、E三点在同一直线上，BC=3，ED=4，则CE= ．
（2）【问题探究】如图，在△ABC中，AB=AC，点D、E是BC边上两点，连接AD，以AD为腰作等腰直角△ADF，∠ADF=90°，作FE⊥BC于点E，FE=CE，若BD=2，CE=5，求△CDF的面积．
（3）【拓展应用】如图3，在△ABC中，∠BAC=90°，AB=AC=13，点G在BC边上，满足∠GAC=3∠BAG，点H在线段AC上，AH=4，点E是直线AC上的一个动点，连接GE，过点G作GF⊥GE，且GE=GF．当点P是线段AG上的一个动点时，连接PH、PF，是否存在PH+PF的最小值？如果存在，请求出PH+PF的最小值；如果不存在，请说明理由．
$德优题库$

共享时间:2024-07-12 难度:1 相似度:2

解析

纠错

下载

组卷白板

196259. （2024•高新一中•七下期末）数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=6，AC=10，D是BC的中点，求BC边上的中线AD的取值范围．
【方法探索】（1）小明在组内经过合作交流，得到了如下的解决方法：如图1，延长AD到点E，使DE=AD，连接BE．根据SAS可以判定△ADC≌△EDB，得出AC=BE．这样就能把线段AB、AC、2AD集中在△ABE中．利用三角形三边的关系，即可得出中线AD的取值范围是．
【问题解决】（2）由第（1）问方法的启发，请解决下面问题：如图2，在△ABC中，D是BC边上的一点，AE是△ABD的中线，CD=AB，∠BDA=∠BAD，试说明：AC=2AE；
【问题拓展】（3）如图3，AD是△ABC的中线，过点A分别向外作AE⊥AB、AF⊥AC，使得AE=AB，AF=AC，判断线段EF与AD的关系，并说明理由．
$德优题库$

共享时间:2024-07-09 难度:1 相似度:2

解析

纠错

下载

组卷白板

196185. （2024•师大附中•九上期末）（1）问题探究：
如图1，在△ABC中，BC=4，∠BAC=45°，则△ABC的外接圆半径为．
（2）问题解决：
如图2，△ABC为一个快递转运中心，∠ABC=90°，AB=BC=30，半径为5的半圆⊙E在△ABC的内部或边上，其圆心E在边BC上．现需在△ABC内建造一个快递堆放平台点P，使∠APC=135°，在半圆⊙E上建造一个快递堆放平台点F，在边AB上建一个快递结算中心Q，为节省转运时间，请求出PQ+FQ的最小值，及取最小值时点P到BC的距离．
$德优题库$

共享时间:2024-02-02 难度:1 相似度:2

解析

纠错

下载

组卷白板

196134. （2024•师大附中•七下期末）【问题背景】
如图1，在等边△ABC中，D、E分别为边BC、AC上任意一点，连接AD、BE，AD与BE相交于点O，且BD=CE．
请直接写出线段AD与BE之间的数量关系：       ；∠AOE=       ．
【推广探究】
如图2，在等边△ABC中，P、M分别为边AB、AC上的点，且AM=BP，过点P作PQ∥BE交AC于点Q，过点M作MN∥AD交BC于点N，PQ与MN交于点F．
（1）∠MFQ=       ；
（2）求证：PQ=MN．
【深入探究】
如图3，在“推广探究”的条件下，令四边形APFM的周长为C₁，四边形CNFQ的周长为C₂，MF=a,FQ=b,FN=c,则C₁-C₂=       （请用含有a、b的代数式表示）．
$德优题库$

共享时间:2024-07-12 难度:1 相似度:2

解析

纠错

下载

组卷白板

cb@dyw.com

2025-04-27

初中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2025年陕西省西安交大附中中考数学四模试卷

更新:2025-04-27 10:54浏览量:41

微信扫码立即登录

AI助手

登录

注册

微信扫码立即登录

AI助手