服务热线
搜题▪组卷
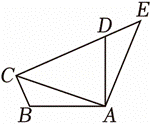
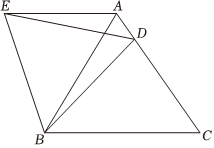在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4，则以下四个结论中：①△BDE是正三角形；②AE∥BC；③△ADE的周长是9；④∠ADE=∠BDC．其中正确的序号是（ ）
+1 
+1 
+1A.绕原点O逆时针旋转90°
B.关于y轴对称
C.绕原点O顺时针旋转90°
D.沿射线AA'的方向平移5个单位
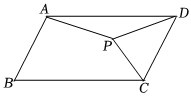如图，在平行四边形ABCD中，∠B=60°，BC=2AB，将AB绕点A逆时针旋转角α（0°＜α＜360°）得到AP，连接PC，PD．给出下面四个旋转角α的度数：①90°；②150°；③180°；④270°．其中能使△PCD为直角三角形的旋转角α的度数为（ ）
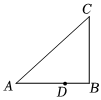如图，在△ABC中，∠A=40°，∠B=90°，点D是AB边上一点，AD=2DB，将△ABC绕点D顺时针旋转α角（0＜α＜180°）得到△A′B′C′，当点A′落在△ABC的边上时，α=（ ）
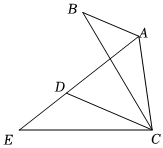如图，在△ABC中，∠BAC=130°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，则旋转角∠ACD的度数为（ ）
lrn@dyw.com
2024-04-24
初中数学 | 八年级下 | 选择题
纠错
收藏
下载
相似
组卷
解析
如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（ ）
如图，将△ABC绕点A按逆时针方向旋转得到△ADE，点B的对应点D恰好落在边BC上．若DE⊥AC，∠E=38°，则∠B的度数为（ ）
如图，△DBE是由△ABC绕点B按逆时针方向旋转40°得到的．若AB⊥DE，则∠A的度数为（ ）
如图，将△AOB绕点O按逆时针方向旋转64°后得到△A′OB，若∠AOB=20°，则∠AOB′的度数是（ ）
如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=25°，则∠B的度数是（ ）
如图，将△ABC绕点A逆时针旋转50°得到△ADE，若∠E=65°且AD⊥BC于点F，则∠BAC的度数为（ ）
如图，△ABC中，∠B=35°，∠BAC=70°，将△ABC绕点A旋转逆时针旋转α度（0＜α＜180）后得到△ADE，点E恰好落在BC上，则α=（ ）
