如图已知直线在图中点在直线上点在直线上点在之间若则如图若平分延长交于点且当时求的度数在的条件下若绕点以每秒转动的速度逆时针旋转一周同时绕点以每秒转动的速度逆时针旋转当转动结束时也随即停止转动在整个转动过程中当秒时

首页 > 试题列表 > 单题解析

179759. （2025•西安三中•七下期中）如图，已知直线AB∥CD．

（1）在图1中，点E在直线AB上，点F在直线CD上，点G在AB，CD之间，若∠1＝28°，∠3＝73°，则∠2＝　　；
（2）如图2，若FN平分∠CFG，延长GE交FN于点M，且∠AEM：∠MEN＝1：2，当

时，求∠CFG的度数；
（3）在（2）的条件下，若AE绕E点以每秒转动4°的速度逆时针旋转一周，同时GF绕F点以每秒转动1°的速度逆时针旋转，当AE转动结束时GF也随即停止转动，在整个转动过程中，当t＝　　秒时，AE∥GF．

共享时间:2025-05-11 难度:3

纠错

下载

相似

组卷白板

[考点]

一元一次方程的应用，角平分线的定义，平行线的判定与性质，

[答案]

（1）45°；

（2）156°；

（3）t＝8或t＝68．

[解析]

解：（1）如图1所示，过G作GH∥AB，

∵AB∥CD，
∴GH∥AB∥CD，
∴∠1＝∠EGH，∠2＝∠FGH，
∴∠1+∠2＝∠EGF，即28°+∠2＝73°，
∴∠2＝45°，
故答案为：45°；
（2）∵FN平分∠CFG，∠AEM：∠MEN＝1：2，
∴可设∠AEM＝α，∠NEM＝2α，∠CFN＝∠GFN＝β，
如图2所示，过G作GP∥CD，过N作NQ∥AB，

∵AB∥CD，
∴NQ∥AB∥CD∥PG，
∴∠QNF＝∠CFN＝β，∠QNE＝∠AEN＝3α，∠PGE＝∠AEM＝α，∠PGF＝∠DFG＝180°﹣2β，
∴∠FNE＝∠QNF﹣∠QNE＝β﹣3α，∠FGE＝∠PGE+∠PGF＝α+180°﹣2β，
∵

，
∴

，
∴β＝78°，
∴∠CFG＝2β＝156°；
（3）如图，根据题意，∠AET＝4t°，∠GFH＝t°，

∵AB∥CD，TE∥HF，
∴∠AET＝∠ETC＝∠HFD＝4t°，
∴4t＝t+180﹣156，
解得：t＝8，
如图，根据题意，∠AEA′＝（360﹣4t）°，∠GFW＝t°，

∵AB∥CD，KE∥WF，
∴∠AEA′＝∠FKE＝（360﹣4t）°，∠WFK+∠FKE＝180°，
∴360﹣4t+t+180﹣156＝180，
解得，t＝68，
综上，t＝8或t＝68，
故答案为：8或68．

[点评]

本题考查了"一元一次方程的应用，角平分线的定义，平行线的判定与性质，"，属于"典型题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

23594. （2020•高新一中•七上期末）如图1，直线DE上有一点O，过点O在直线DE上方作射线OC．将一直角三角板AOB（∠OAB=30°）的直角顶点放在点O处，一条直角边OA在射线OD上，另一边OB在直线DE上方将直角三角板绕点O按每秒10°的速度逆时针旋转一周，设旋转时间为t秒．
（1）当直角三角板旋转到如图2的位置时，OA恰好平分∠COD，此时，∠BOC与∠BOE之间的数量关系为．
（2）若射线OC的位置保持不变，且∠COE=140°．
①则当旋转时间t为6秒时，求∠AOC的度数；
②在旋转的过程中，是否存在某个时刻，使得射线OA，OC与OD中的某一条射线是另两条射线所夹角的角平分线？若存在，请求出所有满足题意的t的取值，若不存在，请说明理由．
$德优题库$

共享时间:2021-03-12 难度:4 相似度:1.67

解析

纠错

下载

组卷白板

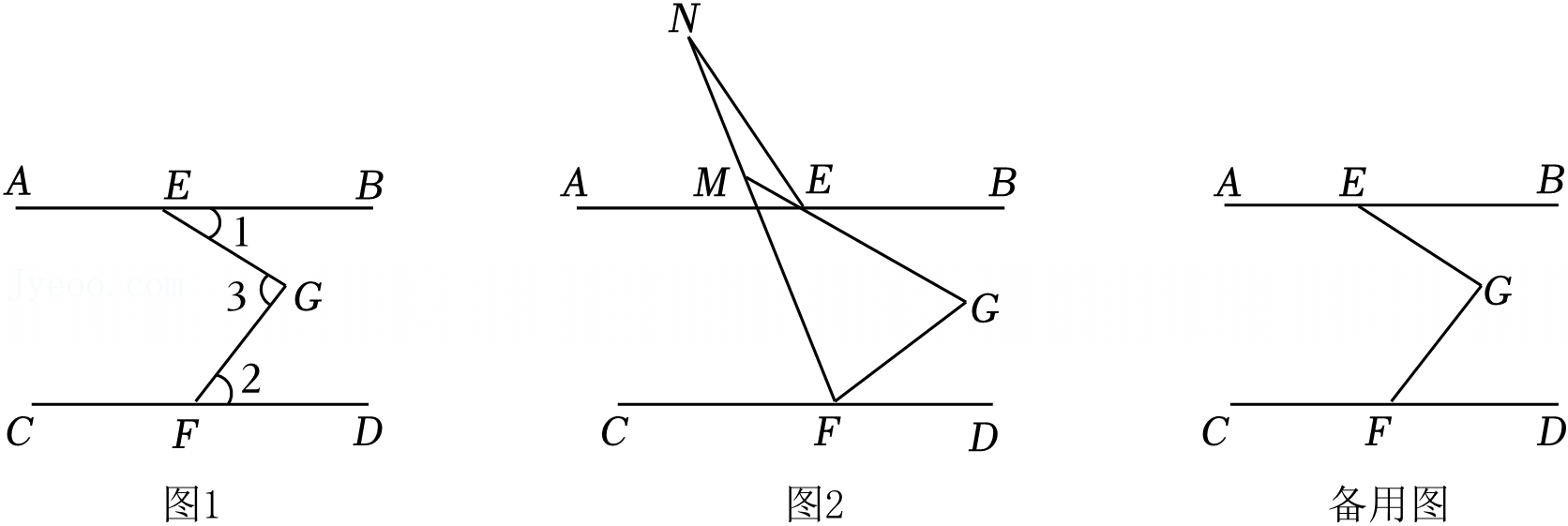
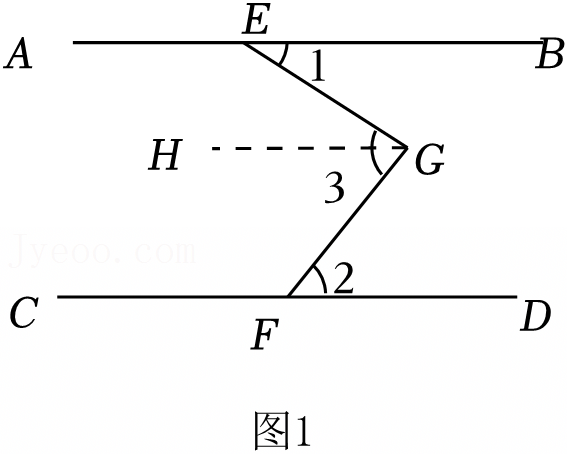
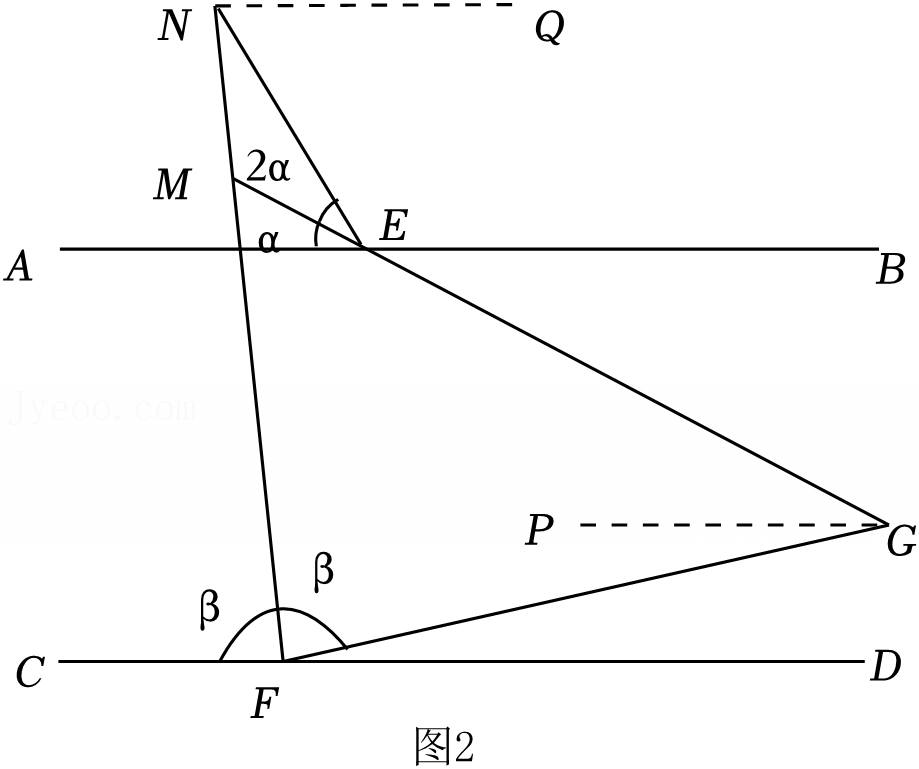
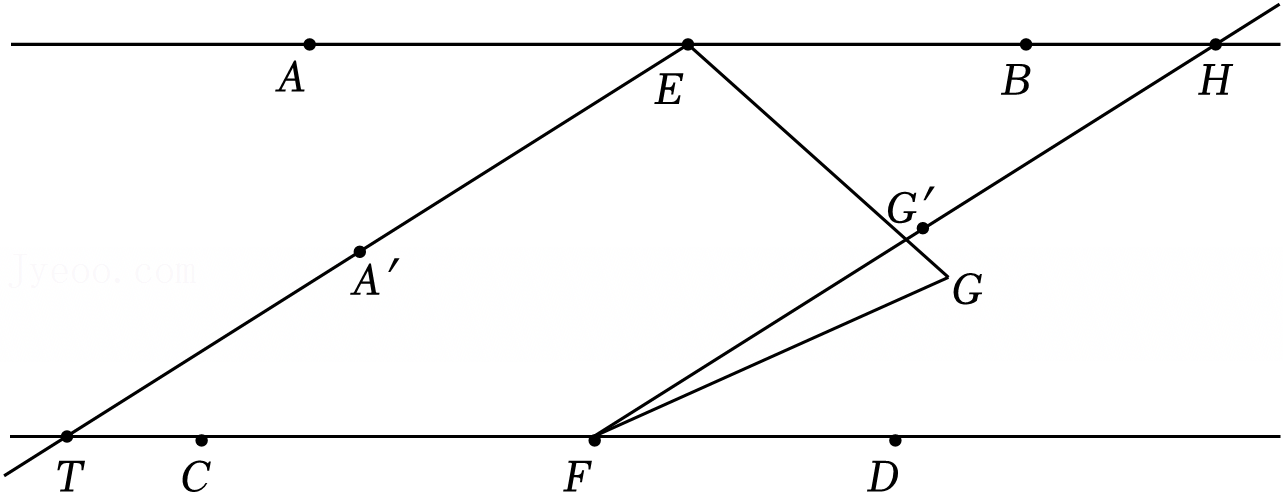
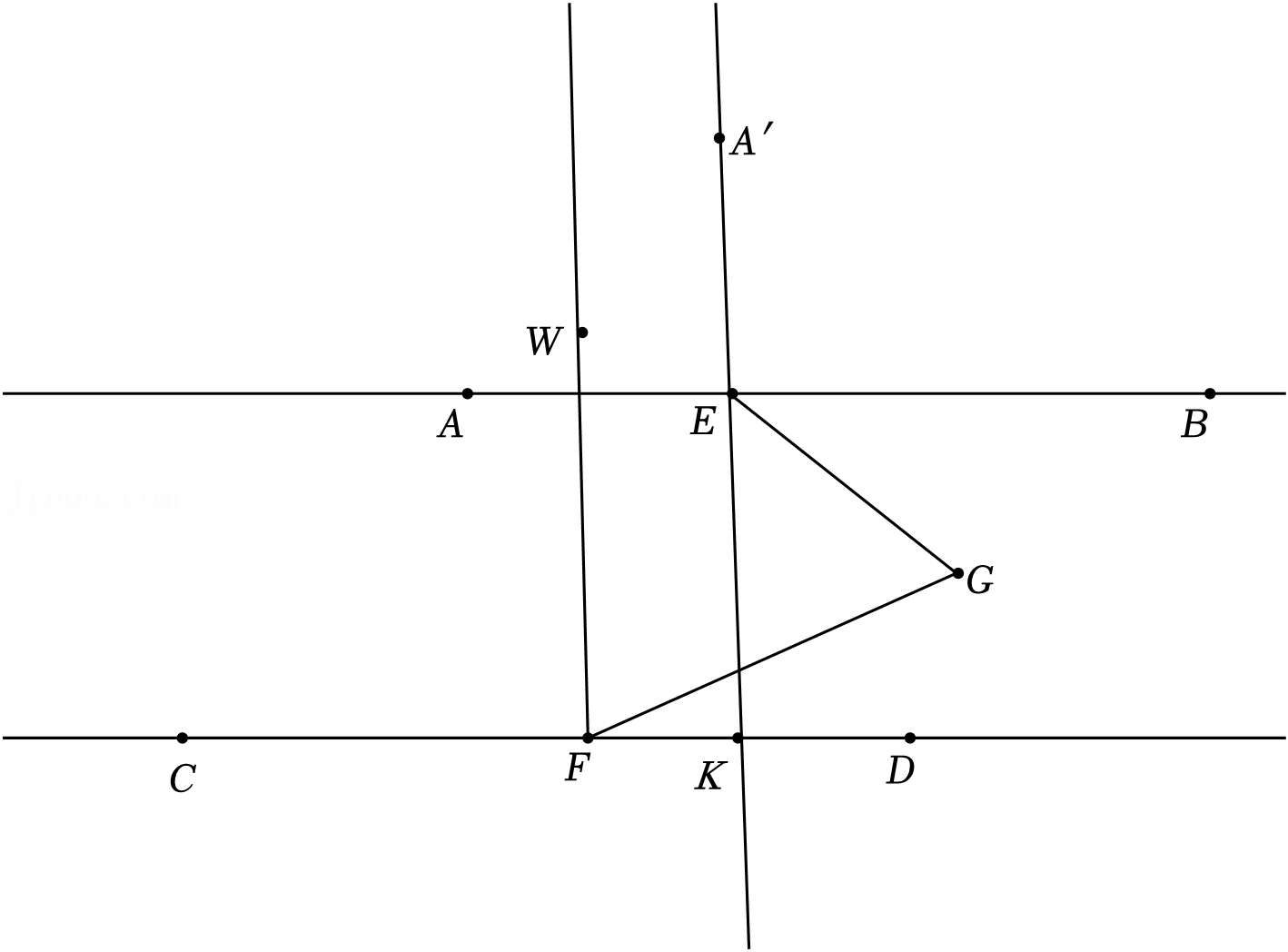
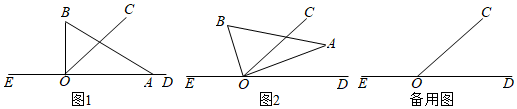
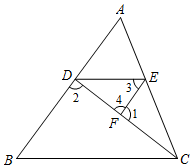
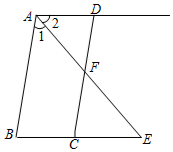24219. （2021•交大附中•七下期中） $德优题库$ 已知：如图，AD∥BC，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E，那么∠B与∠DCE相等吗？试说明理由．请将下面的推理过程补充完整．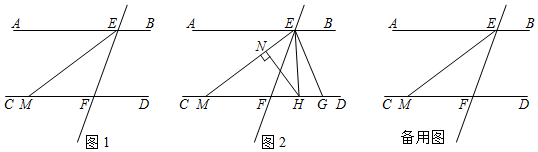
解：∠B=∠DCE，理由如下：
∵AE平分∠BAD（已知），
∴∠1=∠2（角平分线定义），
∵AD∥BC（已知），
∴∠2=∠E（       ），
∴∠1=∠E（       ），
又∵∠CFE=∠E（已知），
∴∠CFE=∠       （等量代换），
∴       ∥       （       ），
∴∠B=∠DCE．

共享时间:2021-05-06 难度:3 相似度:1.67

解析

纠错

下载

组卷白板

61388. （2023•爱知中学•七上期末） $德优题库$ 如图，OD平分∠AOB，OE平分∠AOC，且∠DOE：∠COE=1：4，若∠AOB=90°，求∠AOC的度数．

共享时间:2023-02-19 难度:3 相似度:1.34

解析

纠错

下载

组卷白板

24152. （2021•高新一中•七下期中）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分∠AEF交CD于点M，且∠FEM=∠FME．
（1）猜想直线AB与直线CD有怎样的位置关系？说明你的理由；
（2）若点G为直线CD上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN=α，∠EGF=β．
①如图2，当点G在射线FD上运动时，若β=56°，求α的度数；
②当点G在直线CD上运动时，请直接写出α和β的数量关系．
$德优题库$

共享时间:2021-04-29 难度:5 相似度:1.34

解析

纠错

下载

组卷白板

23589. （2020•高新一中•七上期末）如图，OB是∠AOC的平分线，OD是∠COE的平分线．
（1）若∠AOB=50°，∠DOE=30°，那么∠BOD是多少度？
（2）若∠AOE=160°，∠AOB=50°，那么∠COD是多少度？
$德优题库$

共享时间:2021-03-12 难度:4 相似度:1.33

解析

纠错

下载

组卷白板

61336. （2023•爱知中学•九上期末）某商品进价为200元，若按标价的七五折销售，则利润率为20%，求这件商品的标价．

共享时间:2023-03-02 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

45254. （2024•汇知中学•七下一月）如图，直线AB、CD相交于点O，OE平分∠BOD，∠BOE=30°．求∠AOC的度数．
$德优题库$

共享时间:2024-04-25 难度:1 相似度:1.33

解析

纠错

下载

组卷白板

25679. （2023•陕西省•真题）小红在一家文具店买了一种大笔记本4个和一种小笔记本6个，共用了62元．已知她买的这种大笔记本的单价比这种小笔记本的单价多3元，求该文具店中这种大笔记本的单价．

共享时间:2023-07-20 难度:2 相似度:1.33

解析

纠错

下载

组卷白板

25654. （2024•漳州双语实验学校•七上期末）列方程解决下面问题：
甲、乙两人分别从A，B两地同时出发、沿同一条路线相向匀速行驶，已知出发后3h两人相遇．乙的速度比甲快20km/h、相遇后乙再经1h到达A地．求甲、乙两人的速度．

共享时间:2024-01-28 难度:3 相似度:1.33

解析

纠错

下载

组卷白板

24149. （2021•高新一中•七下期中）如图所示，已知∠1+∠2=180°，∠B=∠3，请你判断DE和BC平行吗？说明理由．（请根据下面的解答过程，在横线上补全过程和理由） $德优题库$
解：DE∥BC，理由如下：
∵∠1+∠4=180°（平角定义），∠1+∠2=180°（已知），
∴∠2=∠4．
∴       ∥       （内错角相等，两直线平行）．
∴∠3=       （       ）．
∵∠3=∠B（已知），
∴       =       （等量代换）．
∴DE∥BC（同位角相等，两直线平行）．

共享时间:2021-04-29 难度:4 相似度:1.33

解析

纠错

下载

组卷白板

23915. （2022•高新一中•二模）某校毕业班准备观看电影《长津湖》，由各班班长负责买票，每班人数都多于40人，票价每张30元，班长小王问售票员买团体票是否可以优惠，售票员说：40人以上的团体票有两种优惠方案可选择，方案一：全体人员可打8折；方案二：若打9折，有5人可以免票，班长小王思考一会儿说，我们班无论选择哪种方案要付的钱是一样的，你知道小王班有多少人吗？

共享时间:2022-03-14 难度:3 相似度:1.33

解析

纠错

下载

组卷白板

23652. （2021•汇知中学•七上期末）根据国家发改委实施“阶梯电价”的有关文件要求，某市结合地方实际，决定从2013年4月1日起对居民生活用电试行“阶梯电价”收费，具体收费标准见下表：

一户居民一个月用电量的范围	电费价格（单位：元/度）
不超过150度	a
超过150度的部分	b

2013年5月份，该市居民甲用电100度，交电费60元；居民乙用电200度，交电费122.5元．
（1）上表中，a= ，b= ；
（2）试行“阶梯电价”收费以后，该市一户居民2013年8月份平均电价每度为0.63元，求该用户8月用电多少度？

共享时间:2022-01-18 难度:4 相似度:1.33

解析

纠错

下载

组卷白板

23616. （2020•交大附中•七上期末）越来越多的人在用微信付款、转账，把微信账户里的钱转到银行卡叫做提现，每个微信账户终身享有1000元的免费提现额度，当累计提现金额超过1000元时，超出的部分需支付0.1%的手续费，以后每次提现支付的手续费均为提现金额的0.1%．
（1）小赵使用微信至今，用自己的微信账户共提现两次，提现金额均为1500元，则小赵这两次提现分别需支付手续费多少元？
（2）小周使用微信至今，用自己的微信账户共提现三次，若小周第三次提现金额恰好等于前两次提现金额的差，提现手续费如表，求小周第一次提现的金额．

	第一次	第二次	第三次
手续费/元	0	1.1	0.2

共享时间:2021-05-13 难度:4 相似度:1.33

解析

纠错

下载

组卷白板

23591. （2020•高新一中•七上期末）某公园门票价格规定如下表：

购票张数	1-50张	51-100张	100张以上
单张票价	13元	11元	9元

某校七年级两个班共104人去游园，其中（1）班有40多人，不足50人，经估算，如果两个班各以班为单位购票，则一共应付1240元．问：
（1）两班各有多少学生？
（2）如果两班联合起来，作为一个团体购票，可省多少钱？

共享时间:2021-03-12 难度:4 相似度:1.33

解析

纠错

下载

组卷白板

1. （2013•邢台市•模拟）某商店积压了100件某种商品，为让这些商品尽快脱手，该商店店主采取了如下销售方案：将标价提高到进价的2.5倍，再作三次降价处理，第一次打出“亏本价”，按标价的七折销售，第二次标出“破产价”，在第一次降价的基础上再降价30%，第三次标出“跳楼价”，是进价的0.98．结果第一次降价处理，仅售出10件；第二次降价处理，售出50件；第三次降价处理，剩下商品被一抢而空．经该店店主核算，这100件商品毛利润为3590元，则该商品的进价是多少元（毛利润＝卖价﹣进价）．

共享时间:2021-05-17 难度:3 相似度:1.33

解析

纠错

下载

组卷白板

hw@dyw.com

2025-05-11

初中数学 | 七年级下 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2024-2025学年陕西省西安三中七年级（下）期中数学试卷

更新:2025-05-11 02:58浏览量:128

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手