服务热线
搜题▪组卷
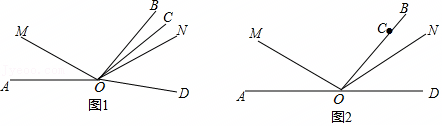
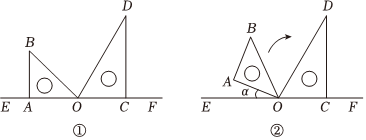
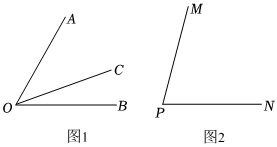 如图1,射线OC在∠AOB的内部,图中有3个角,∠AOB,∠AOC,∠BOC,若其中一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
如图1,射线OC在∠AOB的内部,图中有3个角,∠AOB,∠AOC,∠BOC,若其中一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.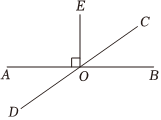 如图,已知OE⊥AB,垂足为O,且直线CD经过点O.
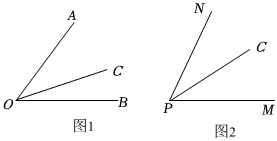
如图,已知OE⊥AB,垂足为O,且直线CD经过点O.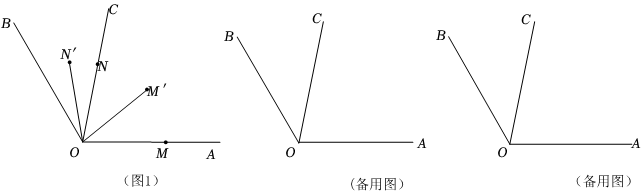
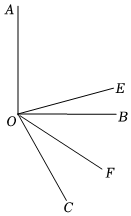 如图,在∠AOC中,射线OE平分∠AOC,点B为∠EOC内部一点,连接OB,射线OF平分∠BOC.
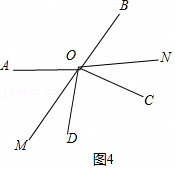
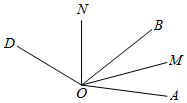
如图,在∠AOC中,射线OE平分∠AOC,点B为∠EOC内部一点,连接OB,射线OF平分∠BOC.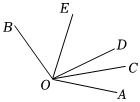 如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.
如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.
th@dyw.com
2024-12-20
初中数学 | 七年级上 | 解答题