服务热线
搜题▪组卷
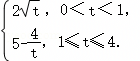 现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰.假设同时使用两种方式给药后,小白鼠血液中药物的浓度等于单独使用每种方式给药的浓度之和.
现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰.假设同时使用两种方式给药后,小白鼠血液中药物的浓度等于单独使用每种方式给药的浓度之和.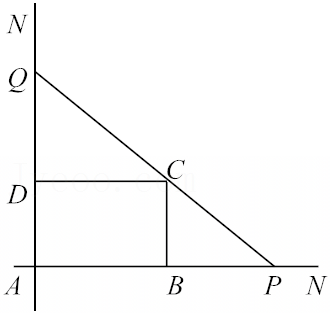
| x/天 | 1 | 2 | 3 | 4 |
| 人数y/个 | 1000 | 1080 | 1166 | 1260 |
| 上市时间x/天 | 2 | 6 | 32 |
| 市场价y/元 | 148 | 60 | 73 |
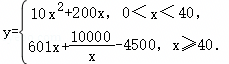 由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
ka@dyw.com
2022-11-10
高中数学 | 高一上 | 解答题