服务热线
搜题▪组卷
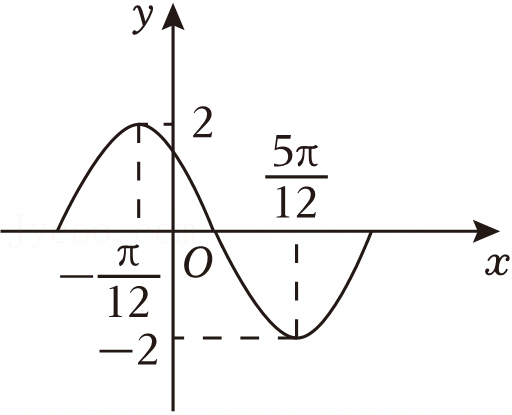
| ωx+φ | x | Asin(ωx+φ) |
| 0 | a=? | 0 |
| 5 | ||
| π | 0 | |
| ﹣5 | ||
| 2π | b=? | 0 |
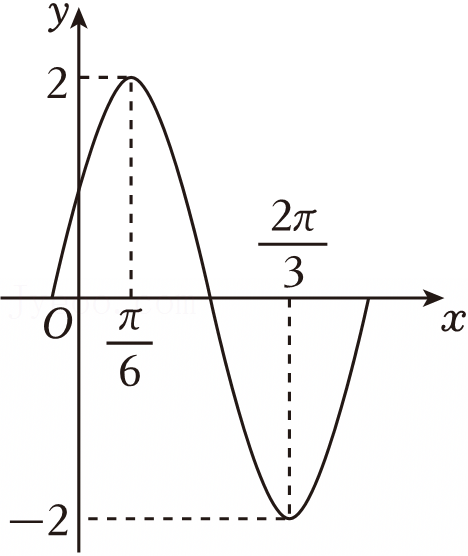
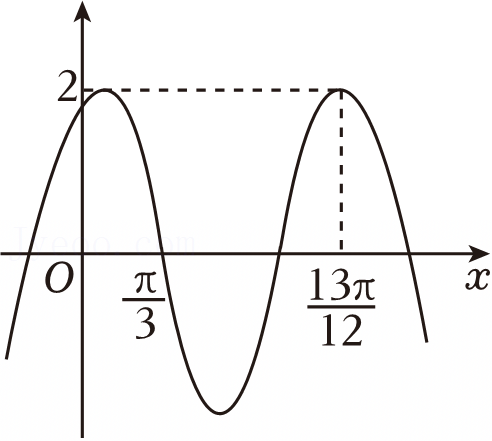
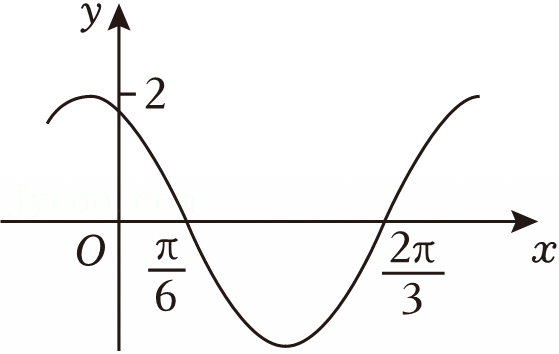
| x | ﹣ |
|||||||
| y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 | 1 |
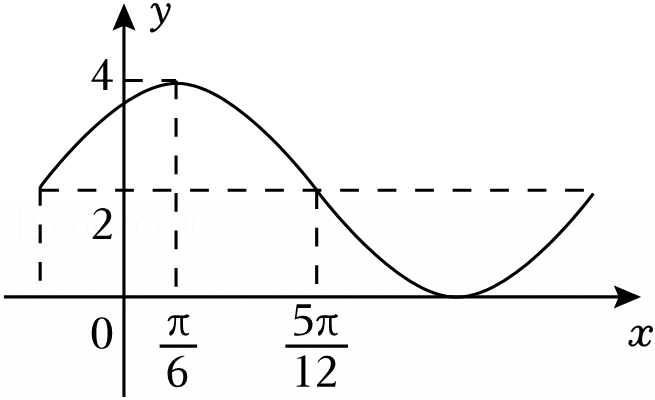
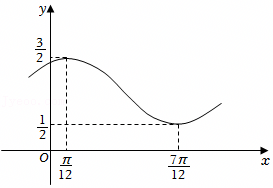
| ωx+φ | 0 | π | 2π | ||
| x | |||||
| Asin(ωx+φ) | 0 | 0 | ﹣2 |

qna@dyw.com
2023-05-18
高中数学 | 高一下 | 解答题