服务热线
搜题▪组卷
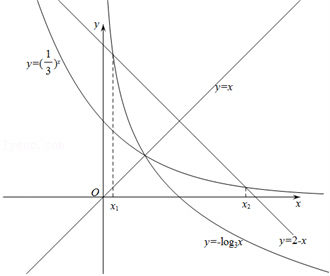
A.f(x)=x2﹣x﹣3
C..f(x)=2x+x
B.![]()
D.f(x)=|log2x|﹣1
A.![]()
B.g(x)=x2﹣x+3
C.![]()
D.![]()
A.f(sin2x)=sinx
C..f(sin2x)=x2+x
B..f(x2+1)=|x+1|
D.f(x2+2x)=|x+1|
A.(﹣∞,﹣1]
C.(0,+∞)
B.(﹣1,0)
D.(﹣∞,0)
A.2a﹣1
C..1﹣2﹣a
B.﹣log2(1+a)
D..log2(1﹣a)
A.(7﹣6ln3,15)
C.(7+6ln3,15)
B.(7,15﹣6ln3)
D.(7,15+6ln3)

dr@dyw.com
2025-04-28
高中数学 | 高二下 | 选择题