如图四边形是圆柱的轴截面是底面圆周上异于的一点则下面结论中正确的序号是填序号平面平面平面

首页 > 试题列表 > 单题解析

167619. （2024•师大附中•十模）如图，四边形ABCD是圆柱的轴截面，E是底面圆周上异于A，B的一点，则下面结论中正确的序号是　　．（填序号）
①AE⊥CE；
②BE⊥DE；
③DE⊥平面BCE；
④平面ADE⊥平面BCE．

共享时间:2024-07-09 难度:2

纠错

下载

相似

组卷

[考点]

直线与平面垂直，平面与平面垂直，

[答案]

①②④．

[解析]

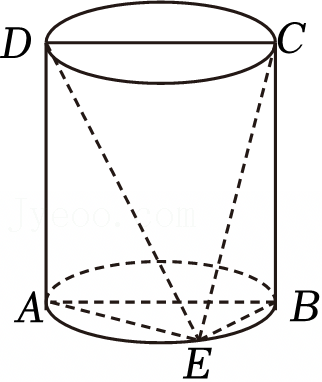
解：因为四边形ABCD是圆柱的轴截面，则线段AB是直径，BC，AD都是母线，
又E是底面圆周上异于A，B的一点，于是得AE⊥BE，
而BC⊥平面ABE，AEC平面ABE，则BC⊥AE，
因为BC∩BE＝B，BC，BE⊂平面BCE，则AE⊥平面BCE，
因为CE⊂平面BCE，因此得AE⊥CE，①正确；
同理，BE⊥DE，②正确；
点D不在底面ABE内，而直线AE在底面ABE内，即AE，DE是两条不同直线，
若DE⊥平面BCE，因为AE⊥平面BCE，与过一点有且只有一条直线垂直于已知平面矛盾，③不正确；
因为AE⊥平面BCE，而AE⊂平面ADE，于是得平面ADE⊥平面BCE，④正确．
故答案为：①②④．

[点评]

本题考查了"直线与平面垂直，平面与平面垂直，"，属于"易错题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

169121. （2020•西工大附中•三模）如图，在正方体ABCD﹣A₁B₁C₁D₁中，AA₁＝3，点M，N分别在棱AB和BB₁上，且D₁M⊥MN，则线段BN的长度的最大值为　

　，此时，三棱锥M﹣ACD₁的体积为　．

共享时间:2020-04-03 难度:2 相似度:1

解析

纠错

下载

组卷

169211. （2025•师大附中•高二上期末）如图所示，在平行四边形ABCD中，E为AB中点，DE⊥AB，DC＝8，DE＝6．沿着DE将△ADE折起，使A到达点A′的位置，且平面A′DE⊥平面BCDE．设P为△A′DE内的动点，若∠EPB＝∠DPC，则P的轨迹的长度为　

共享时间:2025-02-11 难度:2 相似度:1

解析

纠错

下载

组卷

169566. （2024•师大附中•高二下期末）如图，在四棱台ABCD﹣A₁B₁C₁D₁中，底面ABCD为平行四边形，∠BAD＝120°，侧棱AA₁⊥底面ABCD，M为棱CD上的点．AD＝A₁A＝2，A₁B₁＝DM＝1．
（1）求证：AM⊥A₁B；
（2）若M为CD的中点，N为棱DD₁上的点，且

，求平面A₁MN与平面A₁BD所成角的余弦值．

共享时间:2024-07-27 难度:2 相似度:1

解析

纠错

下载

组卷

167232. （2023•周至六中•高二上一月）如图，空间四边形ABCD的各边长均相等，AB⊥AD，BC⊥CD，平面ABD⊥平面CBD，给出下列四个结论：
①AC⊥BD；
②异面直线AB与CD所成的角为60°；
③△ADC为等边三角形；
④AB与平面BCD所成的角为60°．
其中正确结论的序号是　　.（请将正确结论的序号都填上）

共享时间:2023-10-26 难度:3 相似度:0.83

解析

纠错

下载

组卷

dygzsxyn

2024-07-09

高中数学 | | 填空题

下载量
浏览量
收益额

相关试卷 更多>>

2024年陕西师大附中高考数学十模试卷（理科）

更新:2024-07-09 05:34浏览量:8

普通登录

手机登录

微信扫码立即登录