首页 > 试卷详情

德优网2023陕西省西安市莲湖区初中数学考试期末八年级下

2022-2023学年陕西省西安市莲湖区八年级（下）期末数学试卷

试卷总分:120分命题人:csyn@dyw.com 考试时长:120分钟

一、选择题(8小题共24分)

1. （本题3分）下列数学曲线中（不含x,y轴），是中心对称图形的是（　　）

A. $德优题库$

B. $德优题库$

C. $德优题库$

D. $德优题库$

解析

纠错

下载

相似

组卷

2. （本题3分）下列条件中，能判断四边形ABCD是平行四边形的是（　　）

A.AB∥CD，AD=BC	B.∠A=∠B，∠C=∠D
C.AB=AD，CB=CD	D.AB∥CD，AB=CD

解析

纠错

下载

相似

组卷

3. （本题3分）下列从左边到右边的变形中，是因式分解的是（　　）

B.（x﹣y）²＝x²﹣2xy+y²

C.x²﹣1+4k＝（x+1）（x﹣1）+4k

D.a²﹣9＝（a﹣3）（a+3）

解析

纠错

下载

相似

组卷

4. （本题3分）过多边形一个顶点的所有对角线把这个多边形分成了7个三角形，则这个多边形的边数是（　　）

A.8

B.9

C.10

D.11

解析

纠错

下载

相似

组卷

5. （本题3分）若x＞y成立，则下列不等式成立的是（　　）

A.．2x﹣1＞2y﹣1

B.．﹣x+1＞﹣y+1

D.．﹣x＞﹣y

解析

纠错

下载

相似

组卷

6. （本题3分） $德优题库$ 如图，将△ABC沿BC方向平移得到△A'B'C'．连接AA'，若AA'=2.5cm,BC'=10cm,则B'C的长为（　　）

A.3cm

B.4cm

C.5cm

D.6cm

解析

纠错

下载

相似

组卷

7. （本题3分） $德优题库$ 如图，将△ABC绕点A顺时针旋转120°得到△AB'C'，若点C，B，C'共线，则∠B'C'C的度数为（　　）

A.60°

B.45°

C.30°

D.15°

解析

纠错

下载

相似

组卷

8. （本题3分） $德优题库$ 如图，直线y=kx+b交坐标轴于A（-2，0），B（0，1）两点，则不等式-kx-b＞0的解集为（　　）

A.x＞-2

B.x＜-2

C.x＞2

D.x＜2

解析

纠错

下载

相似

组卷

二、填空题(5小题共15分)

9. （本题3分）若分式

的值为0，则x＝　　．

解析

纠错

下载

相似

组卷

10. （本题3分）点（2，-3）关于原点成中心对称的点坐标是．

解析

纠错

下载

相似

组卷

11. （本题3分） $德优题库$ 已知关于x的不等式x-m＞-3的解集如图所示，则m的值为．

解析

纠错

下载

相似

组卷

12. （本题3分） $德优题库$ 如图，在▱ABCD中，BD=4，∠C=∠ABD，则AD的长为．

解析

纠错

下载

相似

组卷

13. （本题3分） $德优题库$ 在Rt△ABC中，∠C=90°，AC=6，BC=8，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN，MN的中点，则DE的最小值是．

解析

纠错

下载

相似

组卷

三、解答题(13小题共81分)

14. （本题5分）分解因式：2m³n-18mn.

解析

纠错

下载

相似

组卷

15. （本题5分）解不等式组

．

解析

纠错

下载

相似

组卷

16. （本题5分）化简：

．

解析

纠错

下载

相似

组卷

17. （本题5分） $德优题库$ 如图，在△ABC中，在BC上找一点E，连接AE，使∠BEA=2∠C．（保留作图痕迹，不写作法）

解析

纠错

下载

相似

组卷

18. （本题5分） $德优题库$ 如图，AC与BD相交于点O，DA⊥AC，DB⊥BC，AC=BD．说明OD=OC成立的理由．

解析

纠错

下载

相似

组卷

19. （本题5分） $德优题库$ 如图，在平面直角坐标系中，已知点A（-2，2），B（-3，6），C（-5，3）．
（1）将△ABC沿着x轴的方向平移得到△A₁B₁C₁，当点C的对应点C₁落在y轴上时，画出△A₁B₁C₁的图形．
（2）将△A₁B₁C₁绕原点O顺时针旋转90°后，点A₁的对应点A₂的坐标是．

解析

纠错

下载

相似

组卷

20. （本题5分） $德优题库$ 如图，在△ABC中，∠C=90°，AB=8，AD是△ABC的一条角平分线．若CD=2.5，求△ABD的面积．

解析

纠错

下载

相似

组卷

21. （本题6分）又是一年瑞阳至，绿杨带雨垂垂重，五色新丝缠角粽．端午节前夕，某超市打算用不超过3000元购买A，B两种品牌的粽子50盒，其中A种品牌粽子的单价是56元，B种品牌粽子的单价是64元，且购买B种品牌的粽子不少于23盒，请你求出所有购买方案．

解析

纠错

下载

相似

组卷

22. （本题7分）已知一个正多边形的边数为n.
（1）若这个多边形的内角和为其外角和的4倍，求n的值．
（2）若这个正多边形的一个内角为108°，求n的值．

解析

纠错

下载

相似

组卷

23. （本题7分）阅读下列材料，并解答相应问题：
对于二次三项式x²+2ax+a²这样的完全平方式，可以用公式法将它分解成（x+a）²的形式，但是对于一般的二次三项式，就不能直接应用完全平方公式了，我们可以在二次三项式中先加上一项，使其配成完全平方式，再减去这项，使整个式子的值不变，例如：
x²+2ax-3a²=x²+2ax+a²-a²-3a²=（x+a）²-（2a）²= ．
（1）用平方差公式补全上面算式最后一步．
（2）用上述方法把m²+6m+8分解因式．

解析

纠错

下载

相似

组卷

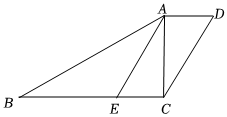24. （本题8分） $德优题库$ 如图，在四边形ABCD中∠ACB=∠CAD=90°，点E在BC上，AE∥DC．
（1）求证：四边形AECD是平行四边形．
（2）若∠B=30°，AE平分∠BAC，AD=2，求四边形AECD的面积．

解析

纠错

下载

相似

组卷

25. （本题8分）某药品生产车间为提高生产效益引进了新的设备，每台新设备每小时包装速度是旧设备包装速度的5倍．经过测试，用1台新设备包装1600盒药品的时间，比4台旧设备包装同样数量的药品节省4小时．
（1）求一台新设备每小时可以包装多少盒药品．
（2）该车间为了每小时完成不少于1000盒药品包装的任务量，决定同时使用新旧两种设备共18台，并且同时开始生产产品，那么至少需要新设备多少台？

解析

纠错

下载

相似

组卷

26. （本题10分）问题提出
（1）如图1，AD是△ABC的高，且BD=CD，则△ABC是三角形．
问题探究
（2）如图2，在▱ABCD中，E是AD的中点，延长BE交CD的延长线于点F．求证：△AEB≌△DEF．
问题解决
（3）如图3，现有一块▱ABCD型板材，E为BC边上的中点，工人师傅要在这块板材开出一个△DEF型凹槽，并要求∠EFB+∠CDE=90°，若DF=13，AF=3，求BF的长度．
$德优题库$

解析

纠错

下载

相似

组卷

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

csyn@dyw.com

2023-07-20

初中数学 | 考试 | 难度:2.23

下载量
浏览量
收益额

下载试卷	收藏
平行组卷	细目重组
试卷分析	加入白板
加卷篮	更多功能

同类试卷 更多>>

2020-2021学年陕西省西安市铁一中学七上数学期末试卷

更新:2021-04-12 07:42浏览量:1087

2020-2021学年陕西省西安市高新一中七上数学期末试卷

更新:2021-03-12 10:33浏览量:1060

2020-2021学年陕西省西安市交大附中七上数学期末试卷

更新:2021-05-13 06:43浏览量:1087

2021-2022学年陕西省西安市汇知中学七上数学期末试卷

更新:2022-01-17 01:05浏览量:2224

2019-2020学年陕西省西安市高新一中七上数学期末试卷

更新:2020-02-17 07:56浏览量:886

2020-2021学年陕西省西安市益新中学九上数学期末试卷

更新:2021-03-28 05:49浏览量:999

2018-2019学年陕西省西安市师大附中八上数学期末试卷

更新:2019-03-02 04:50浏览量:1040

2023-2024学年陕西省西安市爱知中学九年级（上）期末学情检测数学试卷

更新:2024-01-30 03:40浏览量:792

2023-2024学年陕西省西安市新城区爱知中学九年级（上）期末数学试卷

更新:2023-03-02 01:57浏览量:279

2023-2024学年陕西省西安市新城区爱知中学八年级（上）期末数学试卷

更新:2023-02-23 02:53浏览量:316

全选	卷主	序号	卷型	难度	年份	省市区	题源	金币	操作
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看
		8	选择题		2018年	陕西	真题	2币	查看

微信扫码立即登录

AI助手

2022-2023学年陕西省西安市莲湖区八年级（下）期末数学试卷

普通登录

手机登录

微信扫码立即登录

AI助手

2022-2023学年陕西省西安市莲湖区八年级（下）期末数学试卷