服务热线
搜题▪组卷
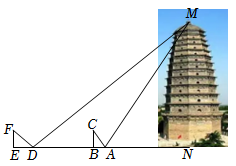小雁塔位于西安市南郊的荐福寺内，又称“荐福寺塔”，建于唐景龙年间，与大雁塔同为唐长安城保留至今的重要标志．小明同学对该塔进行了测量，测量方法如下，如图所示，先在点A处放一平面镜，从A处沿NA方向后退1米到点B处，恰好在平面镜中看到塔的顶部点M，再将平面镜沿NA方向继续向后移动15米放在D处（即AD=15米），从点D处向后退1.6米，到达点E处，恰好再次在平面镜中看到塔的顶部点M、已知小明眼睛到地面的距离CB=EF=1.74米，请根据题中提供的相关信息，求出小雁塔的高度MN﹒（平面镜的大小忽略不计）
＝
，即
＝
①；
＝
，即
＝
②，
＝
，
＝
，
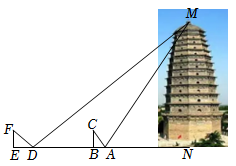
如图，在地面上的点C处放置一块平面镜（镜子大小忽略不计），小华站在BC的延长线上，当小华从平面镜中刚好看到树的顶点A时，测得小华到平面镜的距离CD=2米，小华的眼睛E到地面的距离ED=1.5米；将平面镜从点C沿BC的延长线移动10米到点F处，小华移动到点H处时，小华又刚好在平面镜中看到树的顶点A，这时测得小华到平面镜的距离FH=3米．请根据以上测量过程及数据求出树的高度AB．
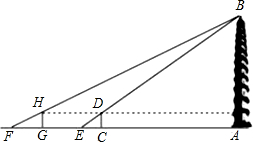西安市的大雁塔又名“慈恩寺塔”，是国家级文物保护单位，玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔，最初五层，后加盖至九层，是西安市的标志性建筑之一，某校社会实践小组为了测量大雁塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，大雁塔的塔尖点B正好在同一直线上，测得EC=4米，将标杆CD向后平移到点G处，这时地面上的点F，标杆的顶端点H，大雁塔的塔尖点B正好在同一直线上（点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得FG=6米，GC=53米，请你根据以上数据，计算大雁塔的高度AB．
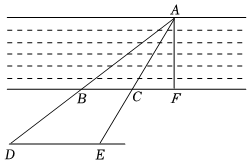
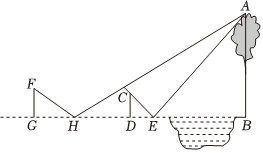在学习了光的反射定律后，数学综合实践小组想利用光的反射定律（反射角等于入射角）测量池塘对岸一棵树的高度AB，测量步骤如下：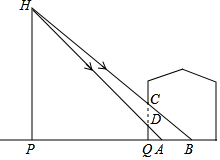
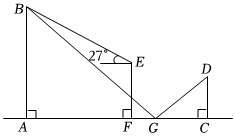周三下午，数学社团的学生在校园进行实践活动，任务是测量校园里玉兰花树AB的高度．小明和小志带着测量工具来到玉兰花树前，小明在空地上选择一点F，把自己的凳子放在F处，站在凳子上测得玉兰花树顶部的仰角为27°，此时小明的眼睛到地面的距离EF=2米．小志走到C处，在自己前方地面的G处放置了一面镜子，恰好能从镜子里看到树的顶端B，此时测得小志的眼睛到地面的距离DC=1.6米．经测量FG=1米，CG=2米，已知点A、F、G、C在同一条直线上，CD⊥AC，EF⊥AC，AB⊥AC，根据以上测量过程及测量数据，请你求出这株玉兰花树AB的高度为多少米．（参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.50）
一数学兴趣小组为了测量校园内灯柱AB的高度，设计了以下方案：在点C处放一面平面镜，从点C处后退到1m点D处，恰好在平面镜中看到灯柱的顶部A点的像；再将平面镜向后移动4m放在F处（即FC=4m），从点F处向后退1.5m到点H处，恰好再次在平面镜中看到灯柱的顶部A点的像，测得眼睛距地面的高度ED、GH均为1.5m,已知点B，C，D，F，H在同一水平线上，且GH⊥FH，ED⊥CD，AB⊥BH．求灯柱AB的高度．（平面镜的大小忽略不计）
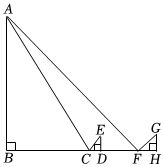
为了测量物体AB的高度，小小带着工具进行测量，方案如下：如图，小小在C处放置一平面镜，她从点C沿BC后退，当退行2米到D处时，恰好在镜子中看到物体顶点A的像，此时测得小小眼睛到地面的距离ED为1.5米；然后，小小在F处竖立了一根高1.8米的标杆FG，发现地面上的点H、标杆顶点G和物体顶点A在一条直线上，此时测得FH为2.6米，DF为3.5米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上．请根据以上所测数据，计算AB的高度．
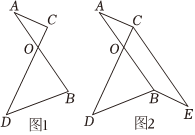线段AB与CD的位置关系如图1所示，AB=CD=m,AB与CD的交点为O，且∠AOC=60°，分别将AB和AC平移到CE，BE的位置（如图2）．
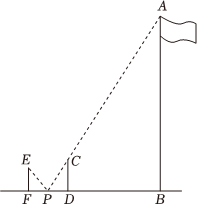小明和小亮同学想利用数学知识测量矗立在广场边上的旗杆AB的高度．如图，他们在广场上的D处放置了一根垂直于地面的标杆CD，然后小明笔直地站在F处，小亮在F和D之间找到一个合适的位置P，并在P点处放置了一面小镜子，此时小明恰好看到在镜子里点A和点C重合．已知，点F、P、D、B在同一条直线上，通过测量，BD=8.8m,FD=2.2m,CD=1.8m,小明的眼睛离地面的高度EF=1.5m.求旗杆AB的高度．
小明为了测量出一深坑的深度，采取如下方案：如图，在深坑左侧用观测仪AB从观测出发点A观测深坑底部P，且观测视线刚好经过深坑边缘点E，在深坑右侧用观测仪CD从测出发点C观测深坑底部P，且观测视线恰好经过深坑边缘点F，点B，E，F，D在同一水平线上．已知AB⊥EF，CD⊥EF，观测仪AB高2m,观测仪CD高1m,BE=1.6m,FD=0.8m,深坑宽度EF=8.8m,请根据以上数据计算深坑深度多少米？
csyn@dyw.com
2023-05-15
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
