服务热线
搜题▪组卷
| A区 | B区 | C区 | D区 | |
| 外来务工人员数x/万人 | 3 | 4 | 5 | 6 |
| 就地过年的人员数y/万人 | 2.5 | 3 | 4 | 4.5 |
．
，该市政府对甲、乙两人的补贴总金额的期望不超过1500元，求p的取值范围．
中斜率和截距的最小二乘估计公式分别为
，
．
，
，
，
，
，则
，
．
，得
，| X | 0 | 1 | 2 |
| P | 2p2﹣4p+2 | ﹣4p2+5p﹣1 | 2p2﹣p |
，又
，
．所以p的取值范围为
．| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
| 零件的横截面积xi | 0.03 | 0.05 | 0.04 | 0.07 | 0.07 | 0.04 | 0.05 | 0.06 | 0.06 | 0.05 | 0.52 |
| 耗材量yi | 0.24 | 0.40 | 0.23 | 0.55 | 0.50 | 0.34 | 0.35 | 0.45 | 0.43 | 0.41 | 3.9 |
，
．
，
．
、
，一小时以上，不超过两小时的概率为
、
，且两人租车时间都不会超过三小时（甲、乙两人租车时间相互独立）．| 树苗序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 高度偏差x | 20 | 15 | 13 | 3 | 2 | ﹣5 | ﹣10 | ﹣18 |
| 直径偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | ﹣0.5 | ﹣2.5 | ﹣3.5 |
，
．
中斜率和截距的最小二乘估计：
，
．
，
．样本方差公式：
．参考数据：
，
，
．
| 生产线 | [53，54） | [54，55） | [55，56） | [56，57） | [57，58） | [58，59） | [59，60] |
| 甲 | 4 | 9 | 23 | 28 | 24 | 10 | 2 |
| 乙 | 2 | 14 | 15 | 17 | 16 | 15 | 1 |
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 6 | 11 | 21 | 34 | 66 | 101 | 196 |
| 支付方式 | 现金 | 乘车卡 | 扫码 |
| 比例 | 10% | 60% | 30% |
，享受8折优惠的概率为
，享受9折优惠的概率为
．根据所给数据以事件发生的频率作为相应事件发生的概率，估计一名乘客一次乘车的平均费用． |
 |
 |
 |
100.54 |
| 62.14 | 1.54 | 2535 | 50.12 | 3.47 |
的斜率和截距的最小二乘估计公式分别为：
，
．
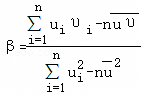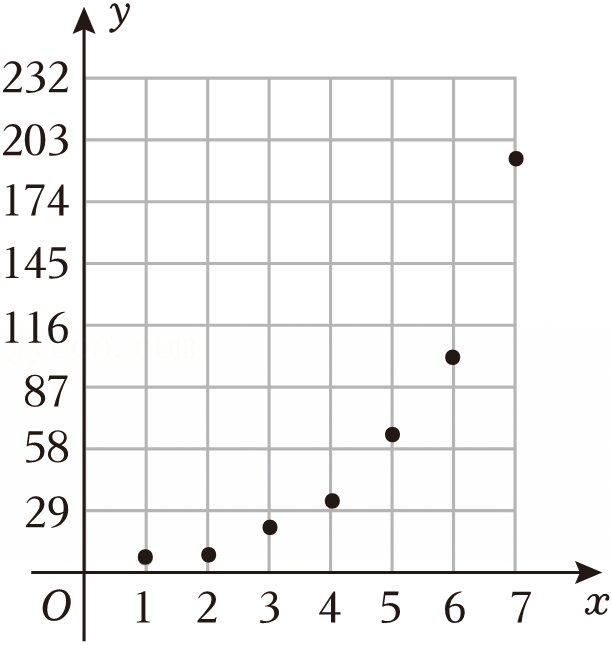
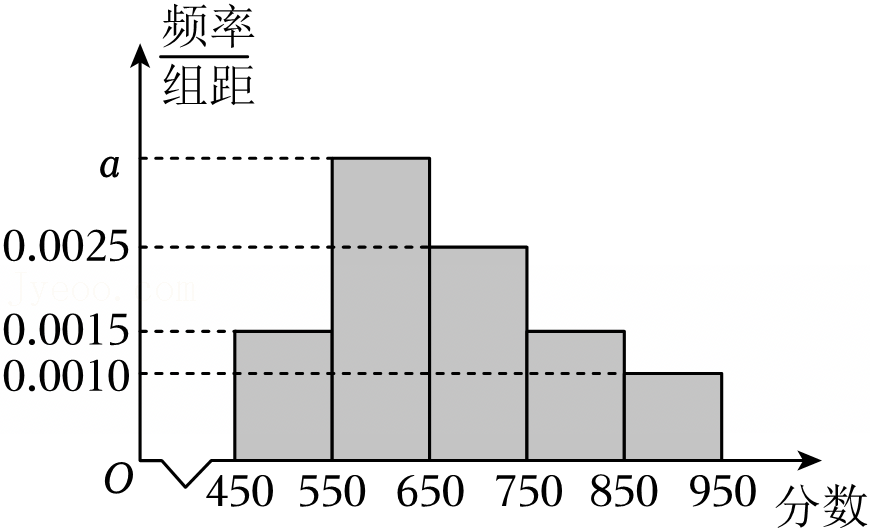
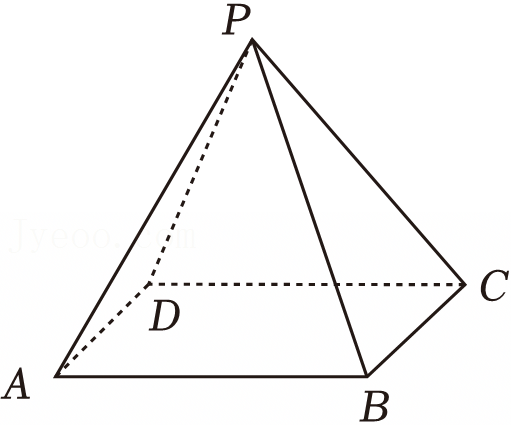
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 用水量y | 2.5 | 3 | 4 | 4.5 | 5.2 |
的斜率和截距的
，
． |
 |
 |
 |
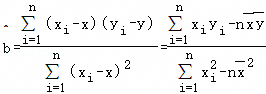| 2.72 | 19 | 139.09 | 1095 |
，
．
＝
，
＝
＝
，
＝
﹣
．
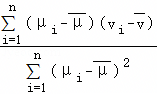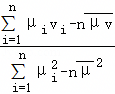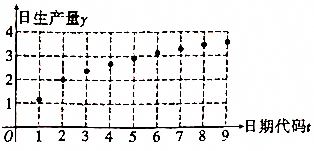
| 年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 需求量y/万吨 | 136 | 146 | 157 | 176 | 186 |
；
＝
，
．
，
；1小时以上且不超过2小时离开的概率分别为
，
；两人滑雪时间都不会超过3小时．
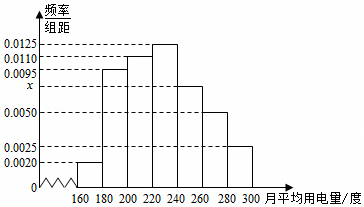
dygzsxyn
2022-12-16
高中数学 | 高三上 | 解答题
纠错
收藏
下载
相似
组卷
解析
