服务热线
搜题▪组卷
．小文在C点处测得楼顶端A的仰角为60°，在D点处测得楼顶端A的仰角为30°（点A，B，C，D在同一平面内）．
≈1.7）
，CD=20m,
=12（m）．
＝
＝
，
,x-16）m,
=
=，，是原方程的解且符合题意，+12≈32（m）．≈1.73，结果精确到0.1m）
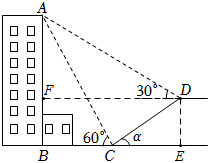
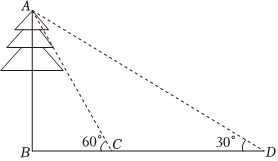
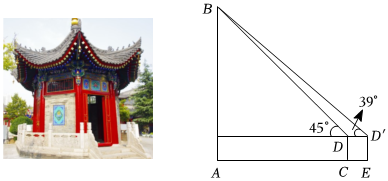
| 活动目的 | 测量建筑物的高度 | |
| 活 动 过 程 |
步骤一：设计测量方案（小组讨论后，画出如图的测量示意图） |  |
| 步骤二：准备测量工具 | 皮尺、测倾器 | |
| 步骤三：实地测量并记录数据（A，B，C，D在同一平面上，CD⊥AD于点D） | ①建筑物CD前有一段斜坡AB，斜坡AB的坡度i＝1：2.4； ②在斜坡AB的底部A测得建筑物顶点C的仰角为31°； ③斜坡AB长52米； ④在点B测得建筑物顶点C的仰角为53°． |
|
| 步骤四：计算建筑物CD的高度 | ||
，
）
米（即CD＝20
米）到达点D处，此时在D处测得楼顶A的仰角为26.7°．（参考数据：sin26.7°≈0.45，cos26.7°≈0.89，tan26.7°≈0.5）
≈1.41，
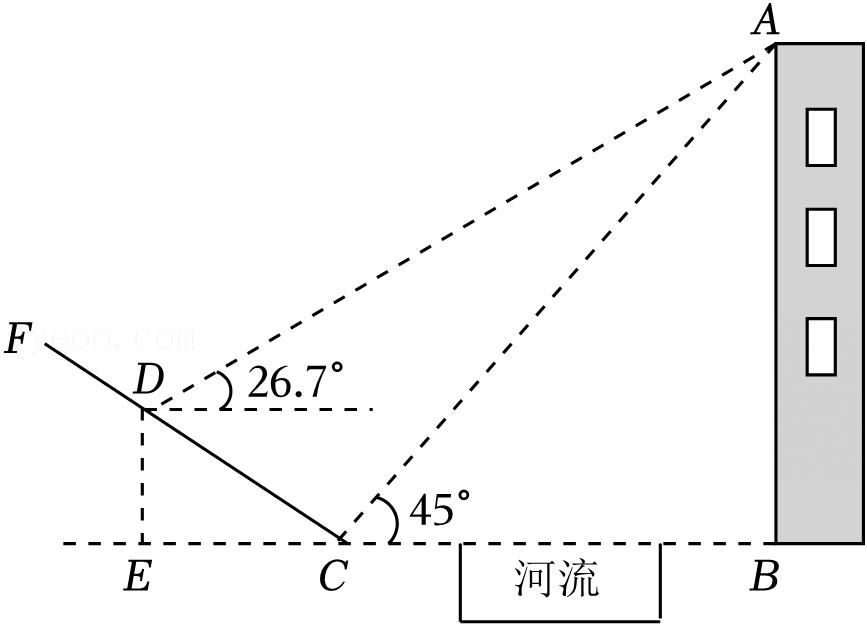
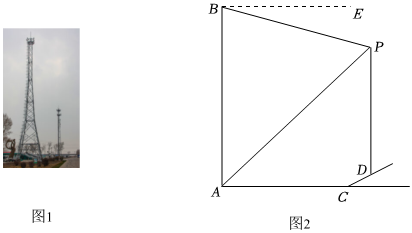
随着农业现代化的进一步推进，新农村的积极建设，农民伯伯可用无人机进行药物喷洒来消灭虫害．如图，这是一位农民伯伯喷药过程中的实时画面示意图，他在水平地面上点A处测得无人机的位置点D的仰角为53°．当他迎着坡度为8：15的斜坡从点A走到点B时，无人机恰好从点D沿着水平方向飞到点C此时，他在点B处测得点C的仰角∠CBE为45°．已知AB=34米，CD=50米，这位农民伯伯让无人机沿与水平地面平行的方向飞行以便喷洒均匀．点A，B，C，D，E，F在同一竖直平面内，求此时无人机的位置点C距水平地面AF的高度．（测角仪的高度忽略不计．参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈
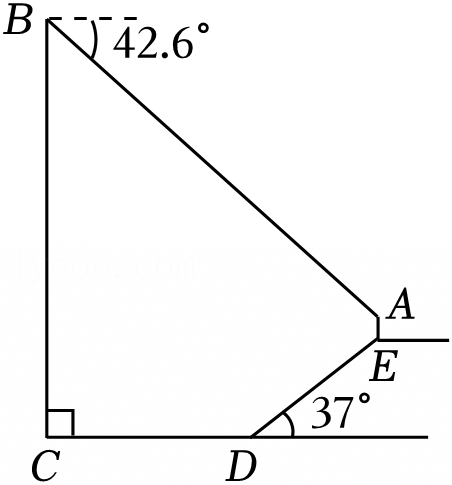
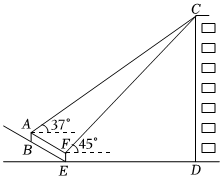我校数学兴趣小组的同学要测量建筑物CD的高度，如图，建筑物CD前有一段坡度为5：12的斜坡EB，小明同学站在斜坡上的B点处，用测角仪测得建筑物屋顶C的仰角为37°，接着小明又向下走了6.5米，刚好到达坡底E处，这时测到建筑物屋顶C的仰角为45°，A、B、C、D、E、F在同一平面内．若测角仪的高度AB=EF=1.4米，求建筑物CD的高度（精确到0.1米，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．
，cos37°≈
，tan37°≈
，sin42.6°≈
，cos42.6°≈
，tan42.6°≈
）
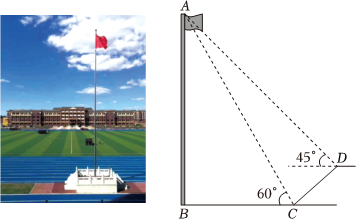
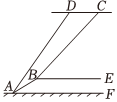
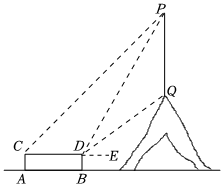如图，小明家对面有一个山坡，一根电线杆PQ直立在山坡上，小明想用学过的数学知识测量电线杆的高度，设计了如下方案：小明在家门口小广场点A处，利用测倾器测得电线杆顶端P的仰角∠PCE=45°，从点A朝着CE方向走8米到达B点，测得电线杆顶端点P的仰角∠PDE=60°，电线杆底端点Q的仰角∠QDE=30°，请根据以上数据计算出电线杆PQ的高度（已知：测倾器的高度AC=BD，AC⊥AB，BD⊥AB，PQ⊥AB，结果保留根号）．
| 测量对象 | 山楂树 |
| 测量工具 | 平面镜、皮尺、测倾器 |
| 测量方案 | ①身高1.5米小华站在点B的位置，让同伴移动平面镜至点C处，此时小华在平面镜内可以看到山楂树顶点E，并测量BC=3米； ②测量平面镜至山脚下的距离CD=14米； ③小华又站在D处，利用测倾器测得山楂树顶的仰角∠EFN=72°． |
| 测量示意图 |  |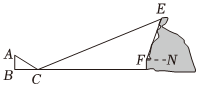
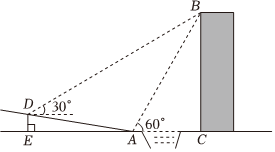如图，某中学数学活动小组同学在学习了“利用三角函数测高”后，想要测量小河对岸一幢建筑物BC的高度，他们先在斜坡上的D处，测得建筑物顶端B的仰角为30°，且D处离地面的高度DE为5m,然后在斜坡的坡底A处测得建筑物顶端B的仰角是60°，已知BC⊥AC，点E，A，C在同一水平线上，斜坡的坡度为1：7，求这幢建筑物BC的高度．（结果保留根号）
rorsczsx
2024-03-12
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
