服务热线
搜题▪组卷
×12×3﹣
×5×10﹣
×8×2＝45，
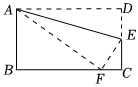如图，已知ABCD是长方形纸片，CD=3，在CD上存在一点E，沿直线AE将△AED折叠，D恰好落在BC边上的点F处，且S△AFB=6，则△AED的面积是 ．
如图，在矩形ABCD中，AB=4，AD=2，E是AB上一个动点，F是AD上一点（点F不与点D重合）．连接EF，将△AEF沿EF翻折，使点A的对应点A′落在边CD上，连接EC，若A′E=CE，则△A′EC的面积为 ．
如图，已知矩形ABCD，AB=2，AD=4，E，F分别为AD，BC边上的动点，且BF=2AE，将四边形ABFE沿EF翻折到四边形EFHG，则CH的最小值为 ．
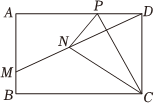如图，矩形ABCD，点P是边AD上一点，连接CP，将△CPD沿CP折叠得△CPN，连接DN并延长交AB于点M，若AM=3BM，AM=3，PD=2，则MN的长为 ．
割补法在我国古代数学著作中称为“出入相补”．著名的数学著作《九章算术》已经能十分灵活地应用“出入相补”原理解决平面图形的面积问题．在《九章算术》中，三角形被称为圭田，圭田术曰：“半广以乘正纵”，也就是说三角形的面积等于底的一半乘高，说明三角形的面积是应用出入相补原理，由长方形面积导出的．如图中的三角形下盈上虚，以下补上．如果图中矩形的面积为20，那么图中阴影部分的面积是 ．
PC+PD的最小值为 ．
，AD＝
，点P为边AB上一点，以DP为折痕将△DAP翻折，点A的对应点为点A′，连接AA′，AA′交PD于点M，点Q为线段BC上一点，连接AQ，MQ，则AQ+MQ的最小值是 ．
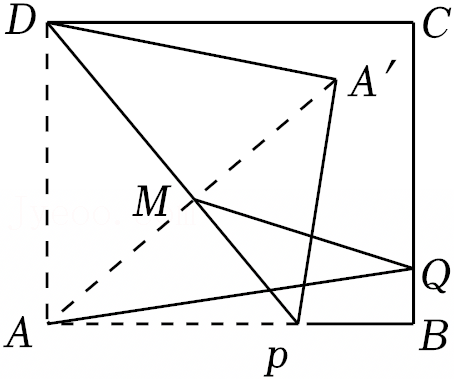
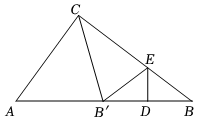如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点D，E分别在AB，BC上，将△BDE沿直线DE翻折，点B的对应点B′恰好落在AB上，连接CB′，若CB′=BB′，则AD的长为 ．
如图，已知A、B两点的坐标分别为（-2，0）、（0，1），⊙C的圆心坐标为（0，-1），半径为1．若D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是 ．
csyn@dyw.com
2023-02-04
初中数学 | 八年级上 | 填空题
如图，将长方形ABCD沿着EF折叠，使得点D恰好落在BC边上的D'处，若BC=12，AB=BD'=8，则△BEF的面积为 ．
纠错
收藏
下载
相似
组卷
解析
如图，矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点D与点B重合，折痕为EF，则△ABE的面积为 ．
如图，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又不重叠的四边形EFGH，若EH=6，EF=8，那么线段AD与AB的比值为 ．
如图，矩形ABCD中，BC=16，CD=12，将△ABE沿BE折叠，使点A恰好落在对角线BD上的F处，则DE= ．
如图，已知△ABC中，∠BAC=120°，点D在边BC上，且AD=4．BD：CD=3：2．当△ABD面积最大时，AB的长为 ．
如图，矩形ABCD中，AB=2，BC=4，AE为∠BAD的角平分线，F为AE上一动点，M为DF的中点，连接BM，则BM的最小值是 ．
