问题提出如图是等边的中线点在的延长线上且则的度数为问题探究如图在中过点作且过点作直线分别交于点求四边形的面积问题解决如图现有一块型板材为钝角工人师傅想用这块板材裁出一个型部件并要求工人师傅在这块板材上的作法如下以点为圆心以长为半径画弧

首页 > 试题列表 > 单题解析

24639. （2022•陕西省•真题）问题提出
（1）如图1，AD是等边△ABC的中线，点P在AD的延长线上，且AP＝AC，则∠APC的度数为　　．
问题探究
（2）如图2，在△ABC中，CA＝CB＝6，∠C＝120°．过点A作AP∥BC，且AP＝BC，过点P作直线l⊥BC，分别交AB、BC于点O、E，求四边形OECA的面积．
问题解决
（3）如图3，现有一块△ABC型板材，∠ACB为钝角，∠BAC＝45°．工人师傅想用这块板材裁出一个△ABP型部件，并要求∠BAP＝15°，AP＝AC．工人师傅在这块板材上的作法如下：
①以点C为圆心，以CA长为半径画弧，交AB于点D，连接CD；
②作CD的垂直平分线l，与CD交于点E；
③以点A为圆心，以AC长为半径画弧，交直线l于点P，连接AP、BP，得△ABP．
请问，若按上述作法，裁得的△ABP型部件是否符合要求？请证明你的结论．

共享时间:2022-06-21 难度:5

纠错

下载

相似

组卷白板

[考点]

线段垂直平分线的定理，三线合一定理，三角形综合题，菱形的性质，正方形的性质，四边形与面积问题，

[校正]

[答案]

答案详见解答

[解析]

解：（1）∵△ABC为等边三角形，
∴AB＝AC，∠BAC＝60°，
∵AD是等边△ABC的中线，
∴∠PAC＝

∠BAC＝30°，
∵AP＝AC，
∴∠APC＝

×（180°﹣30°）＝75°，
故答案为：75°；
（2）如图2，连接PB，

∵AP∥BC，AP＝BC，
∴四边形PBCA为平行四边形，
∵CA＝CB，
∴平行四边形PBCA为菱形，
∴PB＝AC＝6，∠PBC＝180°﹣∠C＝60°，
∴BE＝PB•cos∠PBC＝3，BE＝PB•sin∠PBC＝3

，
∵CA＝CB，∠C＝120°，
∴∠ABC＝30°，
∴OE＝BE•tan∠ABC＝，
∴S_{四边形OECA}＝S_△ABC﹣S_△OBE
＝

×6×3

﹣

×3×

＝

；
（3）符合要求，
理由如下：如图3，过点A作CD的平行线，过点D作AC的平行线，两条平行线交于点F，
∵CA＝CD，∠DAC＝45°，

∴∠ACD＝90°，
∴四边形FDCA为正方形，
∵PE是CD的垂直平分线，
∴PE是AF的垂直平分线，
∴PF＝PA，
∵AP＝AC，
∴PF＝PA＝AF，
∴△PAF为等边三角形，
∴∠PAF＝60°，
∴∠BAP＝60°﹣45°＝15°，
∴裁得的△ABP型部件符合要求．

[点评]

本题考查了"线段垂直平分线的定理,三线合一定理,三角形综合题,菱形的性质,正方形的性质,四边形与面积问题",属于"压轴题"，熟悉知识点是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

考点说明

灰色代表去掉的考点，绿色代表未变动的考点，红色代表新增的考点

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

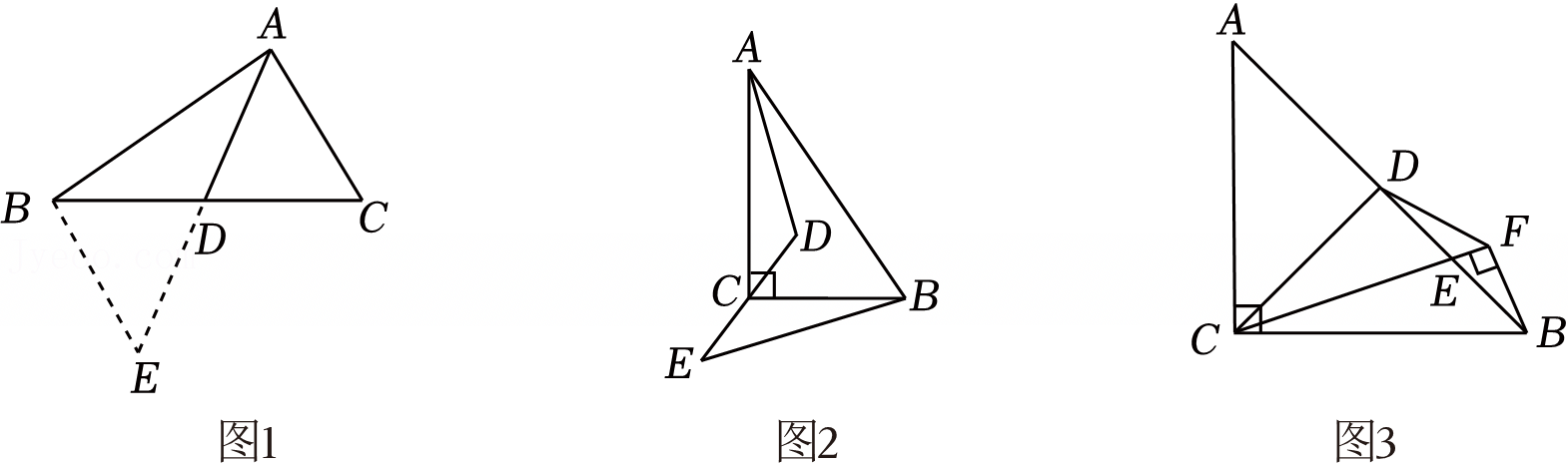
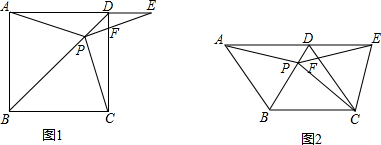
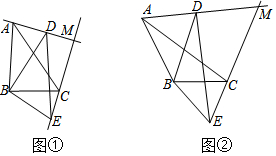
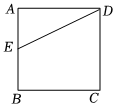283194. （2023•高新一中•三模） $德优题库$ 如图，已知正方形ABCD，点E是AB边上的一点，连接ED．请用尺规作图的方法在线段DE上求作一点F，使得∠BEF+∠BCF=180°（不写作法，保留作图痕迹）．

共享时间:2023-04-02 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

278556. （2025•铁一中学•九模） $德优题库$ 如图，四边形ABCD是正方形，请用尺规作图的方法在CD边上求作一点P，使得PB=2PC．（保留作图痕迹，不写作法）

共享时间:2025-06-20 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

211723. （2025•碑林区•八模）问题提出
（1）如图1，在△ABC中，∠A=90°，AB=6，BC=10，点D在边AB上，过点D作直线l⊥BC，点B与点E关于直线l对称，作CE的垂直平分线m交AC于点F，连接DF．若BD=4，则△ADF的面积为．
问题解决
（2）如图2，在△ABC中，∠A=45°，小明想在△ABC内找一点D，使得点D到A，B，C三点的距离相等，小明进行了2次折叠操作．
第1次：沿着直线m翻折，使得点B与点C重合，展开后，标记折痕m与BC交于点E；
第2次：沿着过点E的直线n翻折，使得点C落在直线m上，点C的对应点为点D．点D到点A，B，C的距离相等吗？请说明理由．
$德优题库$

共享时间:2025-06-11 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

185251. （2024•交大附中•八上期中）【思维启迪】
（1）如图1，AD是△ABC的中线，延长AD到点E．使DE＝AD，连接BE，则AC与BE的数量关系为　　，位置关系为　　．
【思维应用】
（2）如图2，在△ABC中，∠ACB＝90°，点D为△ABC内一点，连接AD，DC，延长DC到点E，使CE＝CD，连接BE，若AD⊥BE，请用等式表示AB，AD，BE之间的数量关系，并说明理由；
【思维探索】
（3）如图3，在△ABC中，∠ACB＝90°，AC＝BC，点D为AB中点，点E在射线DB上（点E不与点B，点D重合），连接CE，过点B作BF⊥CE，垂足为点F，连接FD．若

，BF＝2，请直接写出FD的长．

共享时间:2024-11-29 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

212424. （2025•交大附中•四模）问题探究
（1）如图①，等边△ABC的边长为6，M，N分别是边AC，BC上的点，且满足AM=2，∠CMN=75°，求BN的长；
问题解决
（2）如图②，道路长为120米的BC一侧是一片足够大的学校实践基地，现计划在这片基地上规划一个四边形花园ABCD，按设计要求：点A，B，C，D为出入口，点P为休息厅，现准备过点P规划两条小路AC与BD，且满足∠BPC=120°，AD∥BC，AD=60米，为了满足设计的需要，要使两条小路长度之和最大，请问是否存在符合要求的两条小路？若存在，求出两条小路长度之和（即AC+BD）的最大值，若不存在，请说明理由．
$德优题库$

共享时间:2025-04-27 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

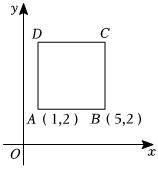277012. （2023•西工大附中•七模） $德优题库$ 如图，在平面直角坐标系中，正方形ABCD的顶点A，B的坐标分别为（1，2），（5，2）．若一次函数y=kx-2（k≠0）的图象经过C点，且与x轴、y轴分别交于点M，N，求△OMN的面积．

共享时间:2023-06-04 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

27732. （2023•爱知中学•八上一月）在本学期的数学学习中，老师提出了这样一个问题：
如图1，在△ABC中，AB=10，AC=6，D是BC的中点，求BC边上的中线AD的取值范围．
【阅读理解】小明在班内经过合作交流，得到了如下的解决方法：
（1）如图1，延长AD到M，使DM=AD，连接BM．根据可以判定△ADC≌△MDB，得出AC=BM．这样就能把线段AB、AC、2AD集中在△ABM中．利用三角形三边的关系，即可得出中线AD的取值范围．
【方法感悟】我们发现，几何图形中出现能表示相等数量关系的条件时，如：“中点”、“角平分线”等，往往可以考虑作“辅助线”，构造全等三角形，从而达到解决问题的目的．
【问题解决】
（2）如图2，在△ABC中，∠B=2∠C，∠BAC的平分线AD交BC边于点D．若AB=3，BD=2，求AC的长．
【应用提升】
（3）已知：如图3，△ABC中，∠A=90°，AB=AC，BC=2．D、E是三角形边AB、AC上两个动点，且AD=CE，连接BE，CD．求（BE+CD）²的最小值．
$德优题库$

共享时间:2023-10-18 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

274897. （2024•西工大附中•八模） $德优题库$ 如图，已知正方形ABCD，请用尺规作图法，在边CD边上求作一点E，使得BE=2CE．（保留作图痕迹，不写作法）

共享时间:2024-06-12 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

274768. （2024•西工大附中•四模）（1）如图①，在四边形ABCD中，∠BAD＝∠BCD＝90°，AC和BD是两条对角线，∠ABD＝30°，过点A作AC的垂线交CD的延长线于点E．求

的值．
（2）炎热的夏天即将到来，水上乐园成为亲子游玩的好去处．某开发公司将在一片浅水湖建造一个大型的水上乐园，并同时开发三条水上商业步行街．如图②，四边形ABCD是项目开发的雏形图，其中A，B，D是三条步行街的入口．AC，BC，DC分别是通向水上乐园C的三条步行街（三条街道宽度相同）．根据仪器测量BD的长约

千米，∠ABD＝30°，∠ADB＝45°．同时根据设计要求还要满足∠BCD＝75°．由于招商类型与环境设计的不同，预计AC段每月平均每千米的租金收入是10万元，BC段每月平均每千米的租金收入是

万元，CD段每月平均每千米的租金收入是20万元．问是否存在一点C，使得三条步行街每月的租金总收入最大．若存在，求出每月租金总收入的最大值，若不存在，请说明理由．

共享时间:2024-04-20 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

286300. （2021•高新一中•七模）问题提出：
（1）如图①，△ABC是等边三角形，AB=6，若点O是△ABC的外心，则OA的长为；
问题探究：
（2）如图②，在四边形ABCD中，AD∥BC．若AD=2，BC=6，对角线AC⊥BD，求四边形ABCD的最大面积；
问题解决：
（3）第十四届全国运动会将在陕西西安举行，秉承“智慧全运迎面来，高科技扮靓十四运”的理念，西安高新一中初中校区steam社团为西安奥体中心设计了一款智能光伏发电零件，可以有效降低能耗，节约能源．如图③，五边形ABCDE为一个新材料结构的光伏发电零件，根据设计要求：AB=40cm,BC=30cm,∠ABC=120°，∠AED=135°，且CD=DE，CD⊥DE．
请你根据以上信息，帮助steam社团的同学们计算这个新材料结构的光伏发电零件的最大面积．
$德优题库$

共享时间:2021-06-02 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

210829. （2025•曲江一中•六模） $德优题库$ 如图，四边形ABCD是正方形，请用尺规作图的方法在CD边上求作一点P，使得PB=2PC．（保留作图痕迹，不写作法）

共享时间:2025-05-19 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

287036. （2021•铁一中学•四模）问题探究：
（1）如图①，已知在△ABC中，BC＝4，则AB的最大值是　　．
（2）如图②，已知在Rt△ABC中，∠ABC＝90°，D为△ABC内一点，且AD＝2

，CD＝6，请求出∠ADB的度数．
问题解决：
（3）如图③，某户外拓展基地计划在一处空地上修建一个新的拓展游戏区△ABC，且AB＝AC．∠BAC＝120°，点P是△ABC内一个打卡点．按照设计要求，CP＝30米，即∠APB＝120°．为保证游戏效果，需要A、P的距离与B、P的距离和尽可能大

共享时间:2021-04-29 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

61367. （2023•爱知中学•八上期末）（1）如图1所示，已知线段OA=4，AB=5，则线段OB长度的最小值为．
（2）如图2所示，△ABC与△ADE均为等腰直角三角形，AB=AC，AD=AE，点C在线段DE上，若DC=4，CE=2，求BC长．
（3）如图3所示，△OAB为等腰三角形，OA=OB=4，以AB为边在其上方作等腰直角△ABC，∠ABC=90°，连接OC，求线段OC的最小值．
$德优题库$

共享时间:2023-02-23 难度:1 相似度:1.17

解析

纠错

下载

组卷白板

181254. （2024•西光中学•八下二月）如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．
$德优题库$

共享时间:2024-06-24 难度:3 相似度:1

解析

纠错

下载

组卷白板

6245. （2017•铁一中学•模拟）如图①，在 Rt△ABC中，AB＝4，BC＝3，将△ABC绕点B顺时针旋转α（0＜α＜120°）得△DBE，连接AD，EC，直线AD、EC交于点M．
（1）当α＝30°时，∠BAD＝　　．
（2）在旋转的过程中，四边形ABCM的面积是否存在最大值？若存在，求出四边形ABCM面积的最大值；若不存在，请说明理由；
（3）如图②，若△ABC中，∠ABC＝120°，其余条件不变，四边形ABCM的面积是否存在最大值？若存在，求出四边形ABCM面积的最大值；若不存在，请说明理由．

共享时间:2017-07-03 难度:5 相似度:0.73

解析

纠错

下载

组卷白板

竹黎

2022-06-21

初中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2022年陕西省中考数学试卷（A）

更新:2022-06-21 02:50浏览量:2368

微信扫码立即登录

AI助手

登录

注册

微信扫码立即登录

AI助手